ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ЗНАКА
Пусть относительно общей декартовой системы координат 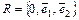 задана прямая
задана прямая  общим уравнением
общим уравнением 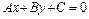
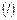 .
.
Рассмотрим функцию 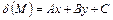 , где
, где 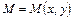 .
.
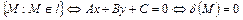 .
.
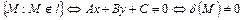 .
.
Выясним смысл неравенств 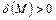 и
и 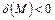 .
.
Пусть 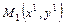 и
и 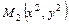 :
: 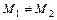 ,
, 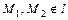 .
.
Говорят, что прямая  делит отрезок
делит отрезок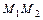 в отношении
в отношении 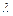 , если в этом же отношении точка пересечения прямых
, если в этом же отношении точка пересечения прямых 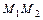 и
и  делит отрезок
делит отрезок 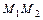 .
.
Пусть точка 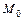 пересечения прямых
пересечения прямых 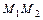 и
и  делит отрезок
делит отрезок 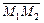 в отношении
в отношении 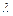 , т.е.
, т.е. 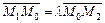 ,
, 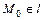 и
и 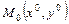 :
:
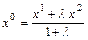 ,
, 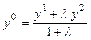 .
.
Тогда
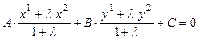
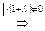
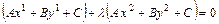 , (*)
, (*)
а поскольку по условию 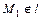 , то
, то 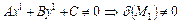 ,
, 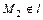 , то
, то 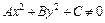
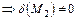 . Поэтому из (*) получаем
. Поэтому из (*) получаем
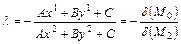 . (7.1)
. (7.1)
Если 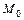 – внутренняя точка отрезка
– внутренняя точка отрезка 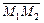 , то
, то 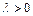 и (7.1)
и (7.1) 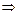
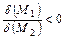 ,
,
т.е. 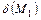 и
и 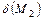 имеют разные знаки.
имеют разные знаки.
Если 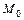 – внешняя точка отрезка
– внешняя точка отрезка 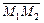 , то
, то 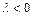 и (7.1)
и (7.1) 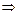
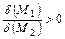 ,
,
т.е. 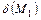 и
и 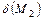 имеют одинаковые знаки.
имеют одинаковые знаки.
Вывод: В точках, расположенных по разные стороны прямой  , линейный трехчлен принимает значения разных знаков. В точках, расположенных по одну сторону от прямой
, линейный трехчлен принимает значения разных знаков. В точках, расположенных по одну сторону от прямой  , линейный трехчлен принимает значения одного знака.
, линейный трехчлен принимает значения одного знака.
Таким образом, всякая прямая 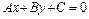 делит плоскость на две полуплоскости так, что в точках одной из них функция
делит плоскость на две полуплоскости так, что в точках одной из них функция 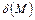 (
(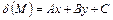 ) принимает положительные значения, а в точках другой – отрицательные.
) принимает положительные значения, а в точках другой – отрицательные.
Определение. Вектор 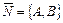 называют главным вектором прямой
называют главным вектором прямой 
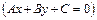 .
.
Очевидно, что 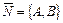 и
и 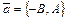 не коллинеарны.
не коллинеарны.
Действительно, допустив противное, получаем
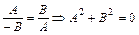 .
.
Получили противоречие.
Отложим теперь главный вектор 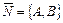 от некоторой точки
от некоторой точки 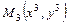 прямой
прямой 
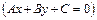 .
.
Пусть 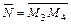 и
и 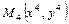 . Т.к.
. Т.к. 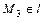 , то
, то 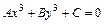 . Тогда
. Тогда 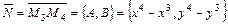
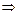
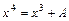 ,
, 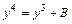
и
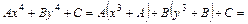
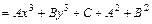
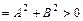 .
.
Следовательно 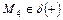 .
.
Вывод: Главный вектор прямой принадлежит положительной полуплоскости, если он приложен к некоторой точке этой прямой.
Замечание: Если прямая не проходит через начало координат, то знаки полуплоскостей определяют с помощью точки 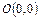 – начала ординат.
– начала ординат.
 2014-02-09
2014-02-09 456
456








