2014-02-09
558
Определение. Ненулевой вектор, перпендикулярный направляющему вектору прямой, называют нормальным вектором прямой.
Пусть относительно прямоугольной декартовой системы координат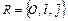 
, задана прямая 
и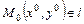 
. И пусть 
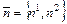и – нормальный вектор прямой .
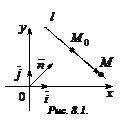Тогда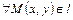 
. 
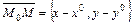– направляющий вектор прямой , и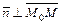 
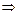
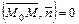
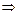
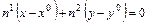. (8.1)
Соотношение (8.1) называют уравнением прямой, проходящей через данную точку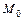 
перпендикулярно данному вектору .
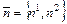Определение. Уравнение прямой называют нормальным, если ее нормальный вектор является единичным.
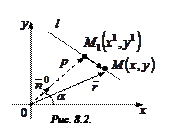Пусть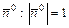 
. Тогда 
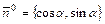. Точка 
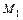– основание перпендикуляра, проведенного из начала координат на прямую .
(
), 
.
. (*)
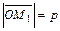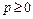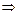
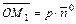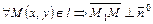
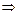
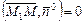Точке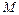 
поставим в соответствие ее радиус-вектор: 
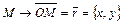. Тогда 
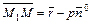. Поэтому (*) 
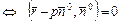или, используя свойства скалярного умножения векторов, получаем
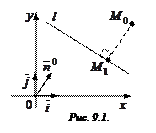
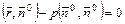
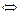
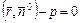. (8.2)
Равенство (8.2) в координатной форме принимает вид
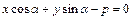. (8.3)
Соотношение (8.3) – нормальное уравнение прямой .
Если в прямоугольной декартовой системе координат прямая задана общим уравнением, то главный вектор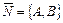 
и направляющий вектор 
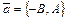взаимно перпендикулярны:
.
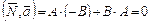Вывод: В прямоугольной декартовой системе координат главный вектор прямой является ее нормальным вектором.
Пусть прямая задана общим уравнением
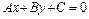. (8.4)
Чтобы привести уравнение (8.4) к нормальному виду, домножим обе его части на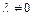 
:
. (**)
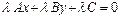Пусть (**) – нормальное уравнение. Тогда
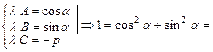
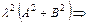
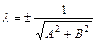. (8.5)
Число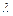 
(8.5) называют нормирующим множителем.
Замечание: Знак 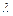выбирают противоположным знаку свободного члена 
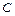общего уравнения прямой.
Тогда (**)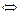
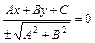. (8.6)
Кроме того, вектор 
имеет координаты
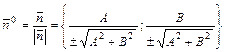. (8.7)
