Функциональные ряды

Основные понятия

Ряд

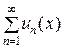= u ₁(х) + u ₂(х) + … + u_n (х) + … (1)

называется функциональным, если его члены являются функциями от х.

Давая х определенные числовые значения, получим различные числовые ряды, которые могут сходится или расходится.

Совокупность значений х, при которых функциональный ряд (1) сходится, называется областью сходимости этого ряда.

Очевидно, что в области сходимости ряда его сумма является некоторой функцией от х. Поэтому сумму функционального ряда обозначают через S (x).

Областью сходимости функционального ряда чаще всего служит некоторый промежуток оси ОХ.

Функциональный ряд (1) сходится (абсолютно) на некотором промежутке, если на этом промежутке сходится ряд .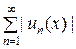

Для определения области сходимости функционального ряда часто используют признаки сходимости Даламбера и Коши.

Пример. Найти область сходимости ряда

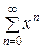= 1 + х + х ² + … + х^п + ….

□

Воспользуемся признаком Даламбера:

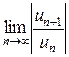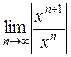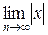= = = | x |.

Ряд сходится, если | x | < 1, т.е. при −1 < x < 1 или х 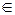(−1; 1).

Следовательно, областью сходимости заданного ряда является интервал (−1; 1).

Для х 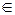(−1; 1) заданный ряд есть бесконечно убывающая геометрическая прогрессия. Тогда, сумма ряда равна

S (x) = 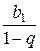= 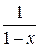, т.е.

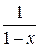= 1 + х + х ² + …+ х^п + ….

■

Пусть S_п (x) – сумма п первых членов ряда (1). Если этот ряд сходится и сумма его равна S (x), то

S (x) = S_п (x) + R_{n +1}(x), (2)

где R_{n +1}(x) – сумма ряда

u_{п +1}(х) + u_{п +2}(х) + …,

т.е.

R_{n +1}(x) = u_{п +1}(х) + u_{п +2}(х) + ….

Сумма R_{n +1}(x) называется остатком ряда (1).

Для любого х из области сходимости Х ряда имеет место соотношение

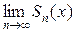= S (x),

поэтому из (2) следует

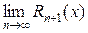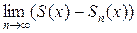= = 0,

т.е. остаток R_{n +1}(x) сходящегося ряда стремится к 0 при п →∞.

Сходимость функционального ряда в каждой точке х из области сходимости Х (х 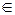Х) называют поточечной сходимостью.

Функциональный ряд 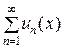называется равномерно сходящимся в некоторой области Х, если для любого 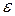> 0 существует номер N такой, что при всех номерах п ≥ N выполняется неравенство

| S (x) − S_n (x)| < 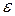(или | R_{n +1}(x)| < )

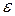для всех 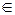х Х.

Различие поточечной и равномерной сходимостей функционального ряда состоит в том, что в первом случае номер N зависит от 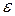и х 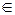Х, т.е. N = N (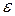, х), а во втором случае − только от 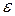, т.е. N = N (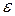). Поточечную сходимость называют также неравномерной.

Теорема. Признак Вейерштрасса (достаточный признак равномерной сходимости функционального ряда)

Если все члены ряда 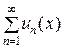удовлетворяют неравенствам

| u_n (х)| ≤ a_n (3)

в некоторой области Х и ряд 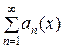(а_п ≥ 0) сходится, то функциональный ряд 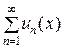сходится равномерно в этой области Х.

○ Так как числовой ряд 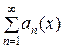сходится, то его остаток R_{n +1}→ 0, т.е. для любого 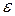> 0 существует номер N такой, что | R_{n +1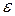}| < при любых п ≥ N.

Согласно неравенству (3),

| R_{n +1}(x)| =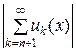≤≤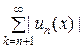 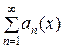= R_{n +1}<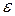

при любых п ≥ N и х 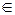Х, т.е. | R_{n +1}(x)| < 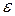при любых п ≥ N и х 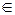Х, а это и означает равномерную сходимость ряда 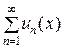в области Х. ●

Числовой ряд 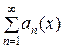, члены которого удовлетворяют неравенствам (3), называется мажорантным рядом или мажорантой для функционального ряда 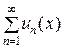, а функциональный ряд 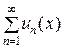в этом случае называется мажорируемым на множестве Х.

Пример. Исследовать ряд на равномерную сходимость

= + + … + + …

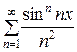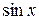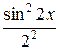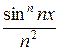на промежутке (−∞,+∞).

□

Так как 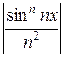≤ 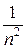, а ряд 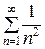сходится (р = 2 > 1), то заданный ряд сходится равномерно при любых значения х. Следовательно, ряд 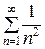является мажорантой для заданного ряда 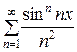, а заданный ряд является мажорируемым на промежутке (−∞,+∞).

■

Замечание 1. Признак Вейерштрасса является только достаточным признаком равномерной сходимости и не является необходимым.

Свойства равномерно сходящихся функциональных рядов

1⁰. Если на множестве Х функциональный ряд 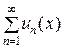с непрерывными членами сходится равномерно, то его сумма S (x) непрерывна на Х.

Замечание 2. Если сумма S (x) функционального ряда с непрерывными членами разрывна в области Х, то сходимость этого ряда заведомо неравномерная в области Х.

2⁰. Если функциональный ряд 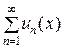с непрерывными членами сходится равномерно в некоторой области Х и имеет сумму S (x), то ряд

+ + … + + …

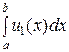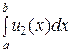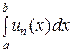сходится и имеет сумму 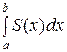, при этом [ a, b ] 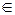X.

Замечание 3. Если функциональный ряд не сходится равномерно, то интегрирование ряда не всегда возможно, т.е.

+ … + + ….

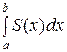
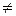
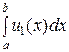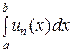Пример. Исследовать сходимость ряда

.

□

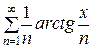Рассмотрим вспомогательный ряд

= + + … + + ….

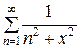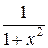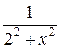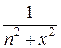Так как 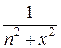≤ 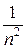для любого х 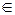R, а ряд 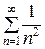сходится, то, по признаку Вейерштрасса, вспомогательный ряд сходится равномерно на все числовой оси. Интегрируя его почленно на отрезке [0, х ], получим

= .

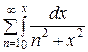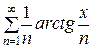Следовательно, по свойству 2⁰, заключаем, что ряд 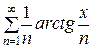сходится (равномерно) на все числовой оси.

■

3⁰. Если ряд 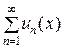с непрерывными дифференцируемыми членами на отрезке [ a, b ] сходится к сумме S (x), а ряд 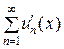сходится равномерно на этом отрезке, то исходный ряд 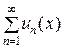сходится равномерно на [ a, b ], его сумма S (x) − непрерывная дифференцируемая функция и справедливо равенство

= .

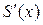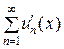Замечание 4. Требование равномерной сходимости ряда производных существенно, и его невыполнение может привести к невозможности почленного дифференцирования ряда.

Пример. Рассмотрим ряд

= + + … + + ….

□

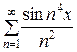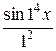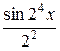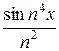Этот ряд равномерно сходится к непрерывной функции при любом х:

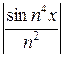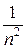≤ , а ряд 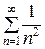сходится (р = 2 > 1).

Напишем ряд, составленный из производных членов исходного ряда:

= = + + … + + ….

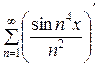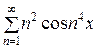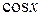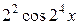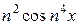Этот ряд расходится. Так, например, при х = 0 он превращается в ряд

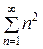= 1 + 2² + 3² + … + п ² + …,

который расходится по следствию к необходимому признаку сходимости числовых рядов:

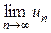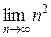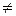= = +∞ 0.

Таким образом, ряд производных не является мажорируемым и, следовательно, заданный ряд нельзя почленно дифференцировать.

■

Степенные ряды

Функциональный ряд вида

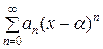= а ₀ + а ₁(х −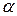) + а ₂(х −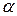)² + … + а_п (х −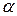) ^п + …, (1)

где а_п, х, 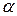− действительные числа, членами которого являются степенные функции, называется степенным рядом по степеням х − 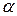; а ₀, а ₁, а ₂,…, а_п − коэффициенты степенного ряда.

При 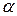= 0 получаем степенной ряд по степеням х

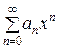= а ₀ + а ₁ х + а ₂ х ² + … + а_пх ^п + …. ()

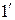Так как ряд (1) заменой х − 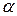= z можно свести к ряду (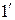), то будем рассматривать степенные ряды вида ().

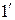Степенной ряд (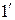) всегда сходится в точке х = 0. При х 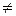0 степенной ряд может сходиться или расходиться.