РЯДЫ
Г
ВЫСШАЯ МАТЕМАТИКА
(ЛЕКЦИИ)
(МК 5)
(Ряды)
Основные понятия
Пусть задана бесконечная числовая последовательность
u 1, u 2, u 3, …, un, ….
Выражение вида
u 1 + u 2 + u 3 + … + un + … =  (1)
(1)
называется числовым рядом.
Числа u 1, u 2, u 3,…, un,… - члены ряда; un – п - й или общий член ряда.
Сумма конечного числа п первых членов ряда называется п - й частичной суммой ряда
Sn = u 1 + u 2 + u 3 + … + un = 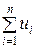
Таким образом,
S 1 = u 1,
S 2 = u 1 + u 2,
S 3 = u 1 + u 2 + u 3,
…………………
Sn = u 1 + u 2 + u 3 + … + un.
Если существует конечный предел
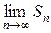 =
= 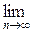
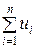 = S,
= S,
то его называют суммой ряда (1), т.е.
S = u 1 + u 2 + u 3 + … + un + … =  ,
,
и говорят, что ряд сходится.
Если предел не существует или равен бесконечности, то говорят, ряд (1) расходится и суммы не имеет.
Пример. Рассмотрим ряд
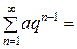 а + aq + aq 2 + … + aqn – 1 + …. (2)
а + aq + aq 2 + … + aqn – 1 + …. (2)
□
Известно, что 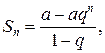 q
q 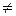 1
1
или
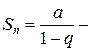
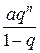 .
.
1) Если | q | < 1, то qn → 0 при п → ∞ и
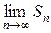 =
= 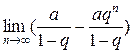 =
= 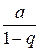 ,
,
т.е. ряд (2) сходится и его сумма 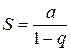 .
.
2) Если | q | > 1, то | qn |→ ∞ при п → ∞. Тогда
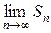 =
= 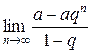 = ± ∞,
= ± ∞,
т.е. предел не существует и ряд (2) расходится.
3) Если q = 1, то ряд (2) имеет вид
а + а + а + …= 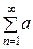 , т.е. Sn = па.
, т.е. Sn = па.
Тогда
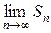 = ∞,
= ∞,
т.е. ряд (2) расходится.
4) Если q = − 1, то ряд (2) имеет вид
а − а + а − а + …= 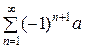 .
.
В этом случае
S = 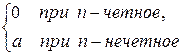 .
.
Таким образом, ряд (2) расходится.
■
Пример. Найти общий член ряда
 +
+ 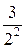 +
+ 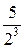 +
+ 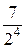 + ….
+ ….
□
Числители членов ряда образуют арифметическую прогрессию: 1, 3, 5, 7, …; п -й член прогрессии находится по формуле
ап = а 1 + d (п – 1).
Имеем а 1= 1, d = 2, поэтому
ап = 2 п – 1.
Знаменатели членов ряда образуют геометрическую прогрессию: 2, 22, 23, 24, …; п -й член этой прогрессии
bn = 2 n.
Следовательно, общий член ряда имеет вид
ип = 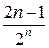 ,
,
т.е.
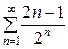 =
=  +
+ 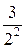 +
+ 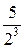 +
+ 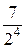 + … +
+ … + 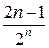 + ….
+ ….
■
Пример. Найти сумму ряда
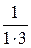 +
+ 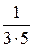 +
+ 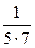 +
+ 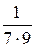 + … +
+ … + 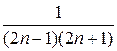 + ….
+ ….
□
Общий член после разложения на простейшие дроби будет иметь вид:
ип = 
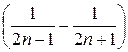 .
.
Тогда
и 1 = 
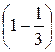 , и 2 =
, и 2 = 
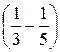 , и 3 =
, и 3 = 
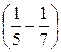 , и 4 =
, и 4 = 
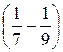 , ….
, ….
Следовательно, сумма п первых членов ряда будет равна
Sn = 
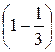 +
+ 
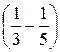 +
+ 
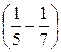 +
+ 
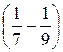 + … +
+ … + 
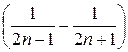 =
=
=  (1 −
(1 − 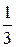 +
+ 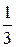 −
− 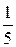 +
+ 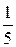 −
− 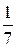 + … +
+ … + 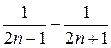 ) =
) = 
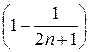 .
.
Теперь найдем сумму ряда
S = 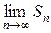 =
= 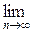

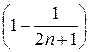 =
= 
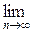
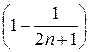 =
=  .
.
Таким образом, сумма ряда S =  и, следовательно, заданный ряд сходится.
и, следовательно, заданный ряд сходится.
■
Свойства числовых рядов
10. Перестановка, отбрасывание или добавление конечного числа членов ряда не влияет на его сходимость (расходимость).
20. Если ряд
а 1 + а 2 + а 3 + … = 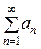 (3)
(3)
сходится и его сумма равна S, то ряд
са 1 + са 2 + са 3 + … = 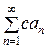 , (4)
, (4)
где 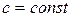 , также сходится и его сумма равна cS.
, также сходится и его сумма равна cS.
○ Пусть Sn = 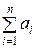 − n -я частичная сумма ряда (3), а
− n -я частичная сумма ряда (3), а
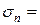 са 1 + са 2 + са 3 + … + сап = с (а1 + а 2 + а 3 + …+ ап) = сSn − п -я частичная сумма ряда (4).
са 1 + са 2 + са 3 + … + сап = с (а1 + а 2 + а 3 + …+ ап) = сSn − п -я частичная сумма ряда (4).
Тогда
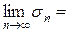
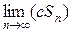 =
= 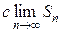 =
= 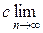
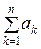 = сS, т.е.
= сS, т.е.
ряд (4) сходится и его сумма равна сS. ●
30. Если ряды
а 1 + а 2 + а 3 + … = 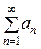 (5)
(5)
и
b 1 + b 2 + b 3 + … = 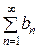 (6)
(6)
сходятся и их суммы соответственно равны Sa и Sb, то ряды
(а 1 + b 1) + (а 2 + b 2) + … = 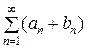 (7)
(7)
и
(а 1 − b 1) + (а 2 − b 2) + … = 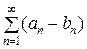 (8)
(8)
Также сходятся и их суммы соответственно равны Sa + Sb и Sa − Sb.
○ Докажем сходимость ряда (7). Пусть S – сумма ряда (7). Тогда
S = 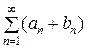 =
= 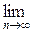
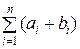 =
= 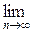 (
(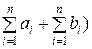 =
= 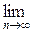
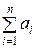 +
+ 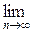
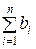 = Sa + Sb.
= Sa + Sb.
Аналогично доказывается, что ряд (8) сходится и его сумма равна Sa − Sb. ●
Замечание 1. Из сходимости рядов 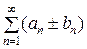 в общем случае не следует сходимость рядов
в общем случае не следует сходимость рядов 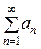 и
и 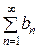 .
.
Замечание 2. Операции суммирования рядов и умножения ряда на число называются линейными операциями над рядами. Отсюда вытекает, что линейные операции над рядами реализуются с помощью линейных операций над их членами.
Необходимый признак сходимости ряда
Теорема. Если ряд  сходится, то
сходится, то
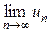 = 0. (9)
= 0. (9)
○ Пусть S = 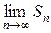 . Так как Sn = Sn− 1 + un, то
. Так как Sn = Sn− 1 + un, то
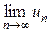 =
= 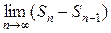 =
= 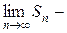
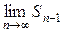 = S − S = 0. ●
= S − S = 0. ●
Следствие. Если условие (9) не выполнено, т.е. предел 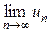 не равен нулю или не существует, то ряд
не равен нулю или не существует, то ряд  расходится.
расходится.
Отметим, что из выполнения условия (9) ещё не следует сходимость ряда: ряд может сходиться или расходиться. Другими словами, условие (9) не является достаточным признаком сходимости ряда.
Пример. □ Для гармонического ряда
1 +  +
+ 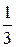 + …+
+ …+ 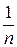 +… =
+… = 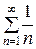 .
.
условие (9) выполняется:
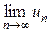 =
= 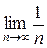 = 0,
= 0,
но гармонический ряд расходится (будет показано ниже). ■
Пример. Исследовать на сходимость ряд
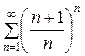 = 21 +
= 21 + 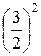 +
+ 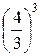 +... +
+... + 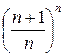 + …
+ …
□
Проверим выполнение условия (9):
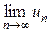 =
= 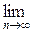
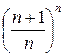 =
= 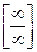 =
= 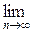
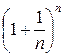 = [1∞] = e
= [1∞] = e 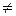 0.
0.
Следовательно, заданный ряд расходится.
■
Знакоположительные ряды
Если задан ряд  с неотрицательными членами ип, то последовательность его частичных сумм является неубывающей. Необходимым и достаточным условиями сходимости такой последовательности является ее ограниченность. Отсюда следует
с неотрицательными членами ип, то последовательность его частичных сумм является неубывающей. Необходимым и достаточным условиями сходимости такой последовательности является ее ограниченность. Отсюда следует
Теорема 1. Для того, чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограниченной.
Признаки сходимости знакоположительных рядов
Признаки сравнения
Пусть заданы два ряда с положительными членами
u 1 + u 2 + u 3 + … + un + … =  (1)
(1)
v 1 + v 2 + v 3 + … + vn + … = 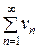 . (2)
. (2)
Теорема 2. Если для членов рядов  и
и 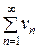 справедливо неравенство
справедливо неравенство
0 ≤ un ≤ vn, (3)
то:
1) из сходимости ряда (2) следует сходимость ряда (1);
2) из расходимости ряда (1) следует расходимость ряда (2).
○ 1. Пусть Sn и 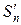 п -ые частичные суммы рядов
п -ые частичные суммы рядов  и
и 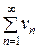 соответственно и ряд
соответственно и ряд 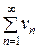 сходится. Из условия (3) следует Sn ≤
сходится. Из условия (3) следует Sn ≤ 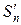 . Тогда, согласно теореме 1, из сходимости ряда
. Тогда, согласно теореме 1, из сходимости ряда 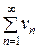 следует ограниченность последовательности {
следует ограниченность последовательности {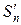 }, а значит, и последовательности { Sn }. Из ограниченности последовательности { Sn } следует сходимость ряда
}, а значит, и последовательности { Sn }. Из ограниченности последовательности { Sn } следует сходимость ряда  .
.
2. Пусть ряд (1) расходится. Тогда последовательность { Sn } неограничена. Следовательно, неограничена и последовательность {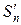 }. Отсюда следует, что ряд (2) расходится. ●
}. Отсюда следует, что ряд (2) расходится. ●
Замечание 1. Теорема 2 справедлива для случая, когда некоторые члены рядов (1) или (2) равны нулю.
Замечание 2. Теорема 2 справедлива для случая, когда условие (3) выполняется, начиная с некоторого номера N.
Замечание 3. Доказанный признак является достаточным для сходимости ряда  и расходимости ряда
и расходимости ряда 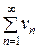 .
.
Пример. Исследовать на сходимость ряд
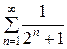 =
= 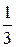 +
+ 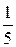 +
+ 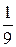 + … +
+ … + 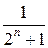 + ….
+ ….
□
Возьмем для сравнения ряд
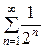 =
=  +
+ 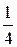 +
+ 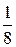 + … +
+ … + 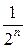 + …,
+ …,
который сходится, т.к. является бесконечно убывающей геометрической последовательностью.
Пусть  =
= 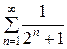 , т.е. ип =
, т.е. ип = 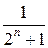 ;
; 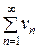 =
= 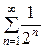 , т.е. vn =
, т.е. vn = 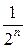 .
.
Условие un < vn, т.е. 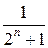 <
< 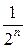 , выполняется при любых п ≥ 1 (знаменатель первой дроби больше знаменателя второй дроби). Следовательно, согласно теореме 2, заданный ряд сходится.
, выполняется при любых п ≥ 1 (знаменатель первой дроби больше знаменателя второй дроби). Следовательно, согласно теореме 2, заданный ряд сходится.
■
Теорема 3 (предельный признак сравнения).
Если существует конечный и отличный от нуля предел
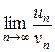 = L
= L 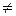 0,
0,
то оба ряда  и
и 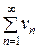 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
○ Из определения предела следует, что для любого  > 0, например 0 <
> 0, например 0 <  < L, найдется номер N, n > N, такой, что
< L, найдется номер N, n > N, такой, что
L −  <
< 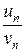 < L +
< L + 
или, т.к. vn > 0,
(L −  ) vn < un < (L +
) vn < un < (L +  ) vn.
) vn.
Из сходимости ряда 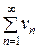 , согласно свойству 20 числовых рядов, следует сходимость ряда
, согласно свойству 20 числовых рядов, следует сходимость ряда 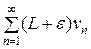 , а значит, по теореме 2 ряд
, а значит, по теореме 2 ряд  сходится.
сходится.
Если ряд 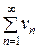 расходится, то расходится ряд
расходится, то расходится ряд 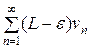 и, следовательно, расходится ряд
и, следовательно, расходится ряд  .
.
Аналогично доказывается, что из сходимости (расходимости) ряда  следует сходимость (расходимость) ряда
следует сходимость (расходимость) ряда 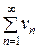 . ●
. ●
Замечание 4. Из доказанного признака следует, что сходимость (расходимость) ряда 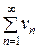 является необходимым и достаточным условием сходимости (расходимости) соответствующего ряда
является необходимым и достаточным условием сходимости (расходимости) соответствующего ряда  и наоборот.
и наоборот.
Пример. Исследовать на сходимость ряд
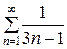 =
=  +
+ 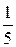 +
+ 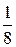 + … +
+ … + 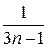 + ….
+ ….
□
Возьмем для сравнения гармонический ряд
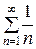 = 1 +
= 1 +  +
+ 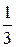 + … +
+ … + 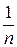 + …,
+ …,
о котором известно, что он расходится. Пусть
 =
= 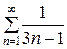 , т.е. ип =
, т.е. ип = 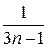 ;
; 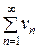 =
= 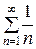 , т.е. vn =
, т.е. vn = 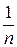 .
.
Найдем предел
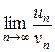 =
= 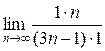 =
= 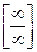 =
= 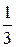
 0.
0.
Следовательно, согласно теореме 3, заданный ряд расходится.
■
Замечание 5. Часто для сравнения используют ряды:
а) 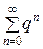 , q > 0, который
, q > 0, который 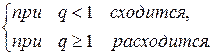
б) 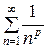 − обобщенный гармонический ряд, который
− обобщенный гармонический ряд, который 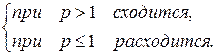
Признаки сравнения не всегда удобно использовать, т.к. для их применения в каждом конкретном случае необходимо подобрать соответствующий вспомогательный ряд, общих конструктивных приемов построения которого не существует. Поэтому на практике часто используют другие признаки, основанные на свойствах членов исследуемого ряда.
Признак Даламбера
Теорема 4. Пусть для ряда  , ип > 0, существует предел
, ип > 0, существует предел
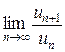 = L. (4)
= L. (4)
Тогда:
1) при L < 1 ряд  сходится;
сходится;
2) при L > 1 ряд  расходится;
расходится;
3) при L = 1 вопрос о сходимости или расходимости ряда остается открытым
(нужны дополнительные исследования).
○ По определению предела из равенства (4) следует, что для любого  > 0, начиная с некоторого номера N, n > N, выполняются неравенства
> 0, начиная с некоторого номера N, n > N, выполняются неравенства
L −  <
< 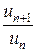 < L +
< L +  . (5)
. (5)
1. Если L < 1, то найдется такое  > 0, что число q = L +
> 0, что число q = L +  < 1. Тогда из неравенства
< 1. Тогда из неравенства
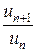 < q при n > N
< q при n > N
следует, что
иN +1 < uN q,
иN +2 < uN +1 q < uN q 2,
……………………..
иN + k < uN + k− 1 q < uN qk.
Так как ряд 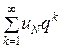 при | q | < 1 сходится, то сходится ряд
при | q | < 1 сходится, то сходится ряд 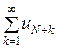 =
=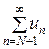 . Следовательно, сходится и ряд
. Следовательно, сходится и ряд  .
.
2. Если L > 1, то найдется такое  > 0, что число q = L −
> 0, что число q = L −  > 1. Тогда из неравенств (5) следует неравенство
> 1. Тогда из неравенств (5) следует неравенство
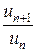 > q при n > N
> q при n > N
или
ип +1 > uп q.
Это означает, что, начиная с номера N, члены ряда возрастают, т.е. необходимый признак сходимости не выполняется, и ряд расходится. ●
Пример. Исследовать на сходимость ряд
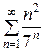 =
= 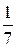 +
+ 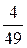 +
+ 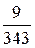 + … +
+ … + 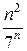 + ….
+ ….
□
Воспользуемся признаком Даламбера:
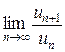 =
= 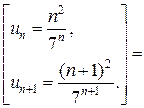
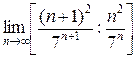 =
= 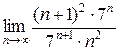 =
=
= 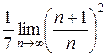 =
= 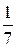 < 1.
< 1.
Следовательно, заданный ряд сходится.
■
Замечание 1. Ряд будет расходится и в том случае, когда 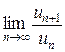 = ∞.
= ∞.
Замечание 2. Если предел 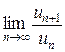 не существует или равен 1, то для исследования на сходимость заданного ряда следует применить какой-либо другой признак сходимости.
не существует или равен 1, то для исследования на сходимость заданного ряда следует применить какой-либо другой признак сходимости.
Замечание 3. Если 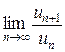 = 1, но отношение
= 1, но отношение 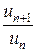 > 1 для всех номеров п, начиная с некоторого, то ряд расходится.
> 1 для всех номеров п, начиная с некоторого, то ряд расходится.
Пример. Исследовать на сходимость ряд
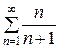 =
=  +
+ 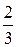 +
+ 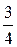 + … +
+ … + 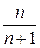 + ….
+ ….
□
Воспользуемся признаком Даламбера:
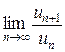 =
= 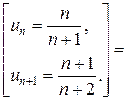
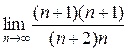 =
= 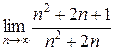 = 1.
= 1.
В данном случае ряд расходится, т.к.
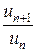 =
= 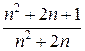 > 1 для любых п.
> 1 для любых п.
■
Признак Коши (радикальный)
Теорема 5. Пусть для ряда  , ип > 0, существует предел
, ип > 0, существует предел
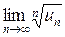 = L. (6)
= L. (6)
Тогда:
1) при L < 1 ряд  сходится;
сходится;
2) при L > 1 ряд  расходится;
расходится;
3) при L = 1 вопрос о сходимости или расходимости ряда остается открытым
(нужны дополнительные исследования).
○ По определению предела из равенства (6) следует, что для любого  > 0, начиная с некоторого номера N, n > N, выполняются неравенства
> 0, начиная с некоторого номера N, n > N, выполняются неравенства
L −  <
< 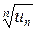 < L +
< L +  . (7)
. (7)
1. Если L < 1, то найдется такое  > 0, что число q = L +
> 0, что число q = L +  < 1. Тогда из неравенств (7) получаем
< 1. Тогда из неравенств (7) получаем
ип < qп при n > N.
Из признака сравнения следует: из сходимости ряда 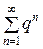 при 0 < q < 1 вытекает сходимость ряда
при 0 < q < 1 вытекает сходимость ряда  .
.
2. Если L > 1, то найдется такое  > 0, что число q = L −
> 0, что число q = L −  > 1. Тогда из неравенств (7) получаем
> 1. Тогда из неравенств (7) получаем
ип > qп при n > N.
Согласно признаку сравнения, из расходимости ряда 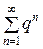 при q > 1 следует расходимость ряда
при q > 1 следует расходимость ряда  . ●
. ●
Замечание 1. Если существует предел 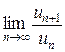 , то существует и предел
, то существует и предел 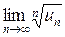 (и они равны между собой). Обратное утверждение не всегда верно. Следовательно, признак Коши “сильнее” признака Даламбера.
(и они равны между собой). Обратное утверждение не всегда верно. Следовательно, признак Коши “сильнее” признака Даламбера.
Замечание 2. Если предел 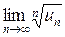 не существует или равен 1, то для исследования на сходимость заданного ряда следует применить какой-либо другой признак сходимости.
не существует или равен 1, то для исследования на сходимость заданного ряда следует применить какой-либо другой признак сходимости.
Пример. Исследовать на сходимость ряд
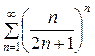 =
= 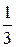 +
+ 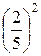 +
+ 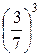 + … +
+ … + 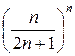 + ….
+ ….
□
Воспользуемся радикальным признаком Коши:
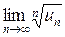 =
= 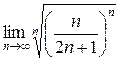 =
= 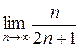 =
=  < 1.
< 1.
Следовательно, заданный ряд сходится.
■
Интегральный признак Коши
Теорема 6. Пусть члены ряда  , ип > 0, не возрастают, т.е.
, ип > 0, не возрастают, т.е.
u 1 ≥ u 2 ≥ u 3 ≥ …, (8)
и пусть f (x) – такая непрерывная невозрастающая функция, что
f (1) = и 1, f (2) = и 2, …, f (п) = ип.
Тогда
1) если несобственный интеграл
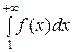
сходится, то сходится ряд  ;
;
2) если указанный интеграл расходится, то расходится и ряд  .
.
○ В силу монотонности функции f (x) для k ≤ x ≤ k + 1 выполняется неравенство f (k) ≥ f (x) ≥ f (k + 1). Интегрируя от k до k + 1, получим
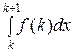 ≥
≥ 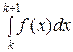 ≥
≥ 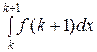
или
иk ≥ 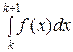 ≥ uk +1,
≥ uk +1,
т.к. f (k) = иk. Распишем полученные неравенства для k = 1, 2, 3, …, n:
и 1 ≥ 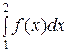 ≥ u 2,
≥ u 2,
и 2 ≥ 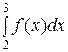 ≥ u 3,
≥ u 3,
…………………..
ип ≥ 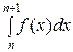 ≥ uп +1.
≥ uп +1.
Суммируя эти неравенства, получим
Sn ≥ 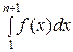 ≥ Sn +1− u 1.
≥ Sn +1− u 1.
1) Пусть интеграл 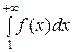 сходится и равен J, тогда
сходится и равен J, тогда 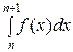 ≤ J и Sn +1 ≤ J + u 1 = C или Sn ≤ C для всех п. Таким образом, монотонно возрастающая последовательность частичных сумм { Sn } ограничена сверху и, следовательно, сходится, т.е. сходится ряд
≤ J и Sn +1 ≤ J + u 1 = C или Sn ≤ C для всех п. Таким образом, монотонно возрастающая последовательность частичных сумм { Sn } ограничена сверху и, следовательно, сходится, т.е. сходится ряд  .
.
2) Пусть интеграл 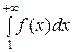 расходится. Тогда, в силу неравенства
расходится. Тогда, в силу неравенства
Sn ≥ 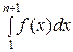
последовательность частичных сумм { Sn } неограниченна, а значит, ряд  расходится. ●
расходится. ●
Замечание 1. Из интегрального признака Коши следует, что сходимость (расходимость) интеграла 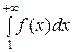 является необходимым и достаточным условием сходимости (расходимости) соответствующего ряда
является необходимым и достаточным условием сходимости (расходимости) соответствующего ряда  .
.
Замечание 2. Нижним пределом несобственного интеграла может быть любое положительное число из области определения функции f (x).
Замечание 3. Теорема справедлива, если неравенства (8) выполняются, начиная с некоторого номера N, т.е. при n ≥ N.
Пример. Исследовать на сходимость ряд
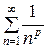 =
= 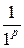 +
+ 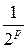 +
+ 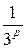 + … +
+ … + 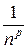 + … − обобщенный гармонический ряд.
+ … − обобщенный гармонический ряд.
□
Используем интегральный признак Коши. Положим f (x) = 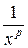 . Функция f (x) монотонно убывает на промежутке [1, +∞).
. Функция f (x) монотонно убывает на промежутке [1, +∞).
1. Пусть р 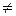 1:
1:
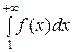 =
=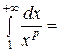
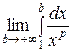 =
=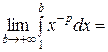
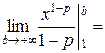
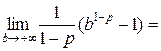
= 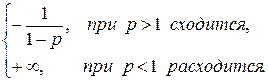
2. Пусть р = 1:
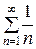 = 1 +
= 1 +  +
+ 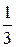 + … +
+ … + 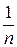 + … − гармонический ряд.
+ … − гармонический ряд.
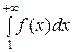 =
=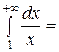
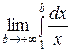 =
=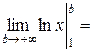
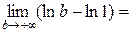 +∞.
+∞.
Следовательно, ряд расходится.
Обобщим полученные результаты:
обобщенный гармонический ряд сходится при р >1 и расходится при р 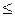 1.
1.
■
Ряд
u 1 + u 2 + u 3 + …+ un + … (1)
называется знакочередующимся, если знаки его членов строго чередуются.
Например,
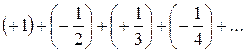 .
.
и 1 и 2 и 3 и 4
Но писать в таком виде ряд неудобно. Поэтому знакочередующийся ряд записывают в виде
1 −  +
+ 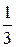 −
− 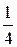 + …,
+ …,
считая, что члены ряда положительные.
Тогда знакочередующийся ряд можно записать в общем виде следующим образом
u 1 − u 2 + u 3 − и 4 + … + (−1) п− 1 ип + … = 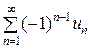 , (
, (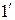 )
)
считая, что ип > 0.
Теорема (признак Лейбница)
Если члены знакочередующегося ряда (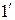 ) удовлетворяют условиям
) удовлетворяют условиям
1) un > un +1 для любых п; (2)
2) 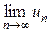 = 0, (3)
= 0, (3)
то ряд (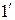 ) сходится, а его сумма S не превосходит первого члена, т.е. S ≤ u 1.
) сходится, а его сумма S не превосходит первого члена, т.е. S ≤ u 1.
○ Рассмотрим четную частичную сумму ряда (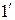 ):
):
S 2 п = (u 1− u 2)+(u 3− и 4)+…+(u 2 n −1− u 2 n ).
Из условия (2) следует, что выражения в скобках больше нуля. Следовательно, последовательность четных частичных сумм { S 2 п } ряда возрастает.
Запишем
S 2 п = u 1 − (u 2 − u 3) − (u 4 − и 5) − … − (u 2 n −2 − u 2 n −1) − u 2 n ≤ u 1. (4)
Из (4) следует, что последовательность { S 2 п } возрастает и ограничена. Следовательно, она имеет предел 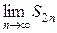 = S при этом S 2 п ≤ u 1.
= S при этом S 2 п ≤ u 1.
Рассмотрим теперь нечетные частичные суммы S 2 п +1. Из соотношения
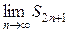 =
= 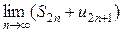 =
= 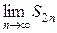 +
+ 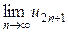 = S + 0 = S.
= S + 0 = S.
Равенство нулю предела 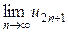 следует из условия (3).
следует из условия (3).
Таким образом, 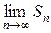 = S, т.е. ряд (
= S, т.е. ряд (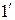 ) сходится, а из неравенства (4) имеем S ≤ u 1. ●
) сходится, а из неравенства (4) имеем S ≤ u 1. ●
Ряд, удовлетворяющий условиям доказанной теоремы, называется рядом Лейбница.
Замечание 1. Признак Лейбница справедлив, если неравенства (2) выполняются, начиная с некоторого номера N, n ≥ N.
Замечание 2. Если u 1 > 0, то сумма знакочередующегося ряда положительна.
Замечание 3. Если знакочередующийся ряд удовлетворяет условиям теоремы Лейбница, то можно оценить погрешность, которая получится при замене суммы ряда S на частичную сумму Sn. При такой замене мы отбрасываем все члены ряда, начиная с un +1, Но отброшенные члены ряда сами образуют знакочередующийся ряд, сумма которого по модулю меньше первого члена этого ряда, т.е. меньше un +1. Значит, погрешность, получающаяся при замене S на Sn, не превосходит по модулю первого из отброшенных членов.
Пример. Исследовать на сходимость ряд
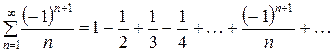 .
.
□
Заданный ряд является знакочередующимся рядом. Воспользуемся признаком Лейбница:
1) 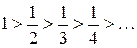
2) 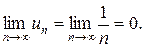
Оба условия теоремы Лейбница выполняются. Следовательно, данный ряд сходится.
Отметим, что сумма п первых членов этого ряда
Sn = 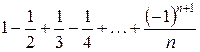
отличается от суммы ряда S на величину, меньшую 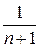 .
.
■
Знакопеременные ряды
Ряд
u 1 + u 2 + u 3 + …+ un + … (1)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные члены.
Очевидно, что знакочередующиеся ряды – частный случай знакопеременных рядов.
Теорема. Достаточный признак сходимости знакопеременного ряда.
Если знакопеременный ряд
u 1 + u 2 + u 3 + …+ un + … (1)
такой, что ряд составленный из абсолютных величин его членов
| u 1| + | u 2| + | u 3| + …+ | un | + …, (2)
сходится, то и данный знакопеременный ряд также сходится.
○ Пусть Sn и 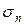 − суммы п первых членов рядов (1) и (2).
− суммы п первых членов рядов (1) и (2).
Пусть 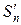 − сумма всех положительных, а
− сумма всех положительных, а 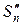 − сумма абсолютных величин всех отрицательных членов среди первых п членов данного ряда (1), тогда
− сумма абсолютных величин всех отрицательных членов среди первых п членов данного ряда (1), тогда
Sn = 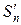 −
− 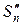 ,
, 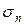 =
= 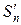 +
+ 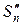 .
.
По условию, последовательность {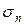 } имеет предел, т.е.
} имеет предел, т.е. 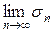 =
= 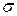 . Последовательности {
. Последовательности {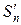 } и {
} и {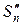 } возрастающие и ограничены числом
} возрастающие и ограничены числом 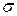 . Следовательно, они имеют пределы
. Следовательно, они имеют пределы
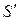 и
и 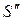 . Из соотношения Sn =
. Из соотношения Sn = 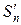 −
− 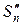 следует, что и { Sn } имеет предел
следует, что и { Sn } имеет предел
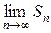 =
= 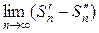 =
= 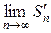 −
− 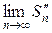 =
= 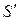 −
− 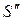 .
.
Это и означает, что ряд (1) сходится. ●
Таким образом, исследование сходимости знакопеременного ряда сводится к исследованию сходимости знакоположительного ряда.
Замечание 1. Доказанный признак является только достаточным признаком сходимости, т.е. обратное утверждение в общем случае не имеет места.
Пример. Исследовать на сходимость ряд
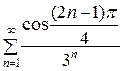 =
= 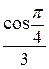 +
+ 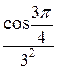 + … +
+ … + 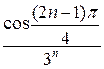 + …. (а)
+ …. (а)
□
Заданный ряд является знакопеременным рядом. Обозначим общий член ряда ип = 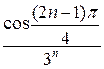 . Построим ряд из абсолютных величин членов заданного ряда:
. Построим ряд из абсолютных величин членов заданного ряда:
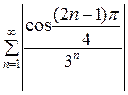 =
= 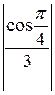 +
+ 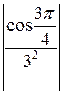 + … +
+ … + 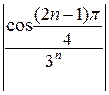 + …. (б)
+ …. (б)
Тогда | ип | = 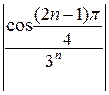 . Исследуем ряд (б) на сходимость. Для этого воспользуемся признаком сравнения, взяв для сравнения ряд
. Исследуем ряд (б) на сходимость. Для этого воспользуемся признаком сравнения, взяв для сравнения ряд
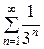 =
= 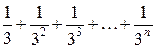 + …. (с)
+ …. (с)
Обозначим vn = 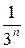 =
= 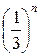 . Ряд (с) сходится, т.к. представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем q =
. Ряд (с) сходится, т.к. представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем q = 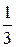 .
.
Сравним члены рядов (б) и (с), т.е. | ип | и vn:
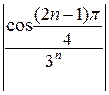 ≤
≤ 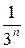 для всех п, т.к.
для всех п, т.к.
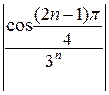 =
= 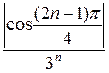 , а
, а 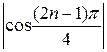 ≤ 1 для любых п, т.е.
≤ 1 для любых п, т.е.
| ип | ≤ vn. Значит ряд (б), составленный из абсолютных величин членов заданного ряда (а), сходится. Тогда, согласно доказанной теореме, заданный ряд (а) сходится.
■
Знакопеременный ряд (1) называется абсолютно сходящимся, если сходится ряд (2). Если же ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся или неабсолютно сходящимся.
Тогда, доказанную теорему можно сформулировать следующим образом: всякий абсолютно сходящийся ряд есть ряд сходящийся.
Пример. Исследовать ряд на абсолютную и условную сходимость:
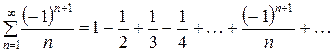 .
.
□
Заданный ряд является знакопеременным рядом, т.к. знакочередующийся ряд является частным случаем знакопеременного ряда. Проверим данный ряд на абсолютную сходимость. Составим ряд из абсолютных величин членов заданного ряда и исследуем его сходимость:
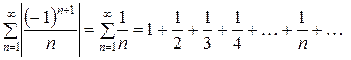 .
.
Построенный ряд является гармоническим рядом, который расходится.
Исследуем заданный ряд на условную сходимость. Заданный ряд является знакочередующимся рядом. Используем теорему Лейбница:
1) 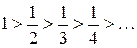 ;
;
2) 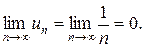


Следовательно, данный ряд сходится.
Вывод: заданный ряд сходится условно.
■
Свойства абсолютно сходящихся и условно сходящихся рядов
10. Если ряд абсолютно сходится, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
20. Если ряд сходится условно, то, какое бы мы не задали число А, можно так переставить члены этого ряда, что его сумма будет равна числу А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки, окажется расходящимся.
30. Если ряды
u 1 + u 2 + u 3 + …+ un + …
и
v 1 + v 2 + v 3 + …+ vn + …
сходятся абсолютно и имеют соответственно суммы S 1 и S 2, то сходится абсолютно и ряд
u 1 v 1 + (u 1 v 2 + u 2 v 1) + (u 1 v 3 + u 2 v 2 + u 3 v 1) + … + (u 1 vn + u 2 vn− 1 + … + unv 1) + ….
Полученный ряд называется произведением рядов (по Коши) и его сумма равна S 1 S 2.
 2014-02-09
2014-02-09 4261
4261