1. Если степенной ряд (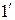 ) сходится при некотором значении х 0
) сходится при некотором значении х 0 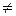 0, то он сходится абсолютно при всяком значении х, для которого | x | < | x 0|;
0, то он сходится абсолютно при всяком значении х, для которого | x | < | x 0|;
2. если ряд расходится при некотором значении 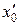 , то он расходится при всяком х, для которого | x | > |
, то он расходится при всяком х, для которого | x | > |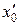 |.
|.
○ 1. Так как по предположению числовой ряд 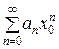 сходится, то
сходится, то 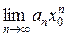 = 0, и, следовательно, существует такое число М >0, что | аn
= 0, и, следовательно, существует такое число М >0, что | аn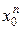 |< M для любых п
|< M для любых п 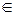 N. Пусть | x | < | x 0|, тогда
N. Пусть | x | < | x 0|, тогда
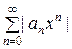 =
= 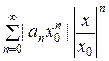 ≤
≤ 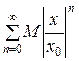 .
.
Члены ряда 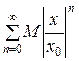 представляют собой бесконечно убывающую геометрическую прогрессию со знаменателем
представляют собой бесконечно убывающую геометрическую прогрессию со знаменателем 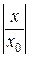 < 1, т.е. этот ряд сходится. Следовательно, ряд
< 1, т.е. этот ряд сходится. Следовательно, ряд
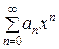 в точке х
в точке х 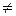 0 сходится абсолютно.
0 сходится абсолютно.
2. Если бы в какой-либо точке х, удовлетворяющей неравенству | x | > |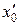 |, ряд сходился, то в силу доказанной первой части теоремы он должен был бы сходиться и в точке
|, ряд сходился, то в силу доказанной первой части теоремы он должен был бы сходиться и в точке 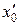 , т.к. |
, т.к. |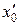 | < | x |. Но это противоречит условию, что в точке
| < | x |. Но это противоречит условию, что в точке 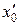 ряд расходится. Следовательно, ряд расходится и в точке х. ●
ряд расходится. Следовательно, ряд расходится и в точке х. ●
Из теоремы Абеля следует, что если степенной ряд (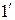 ) сходится хотя бы в одной точке х
) сходится хотя бы в одной точке х 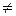 0, то всегда существует число R > 0 такое, что степенной ряд сходится абсолютно для всех | x | < R или х
0, то всегда существует число R > 0 такое, что степенной ряд сходится абсолютно для всех | x | < R или х 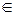 (− R, R) и расходится для всех | x | > R или х
(− R, R) и расходится для всех | x | > R или х 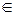 (−∞; − R)
(−∞; − R)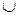 (R; +∞)
(R; +∞)
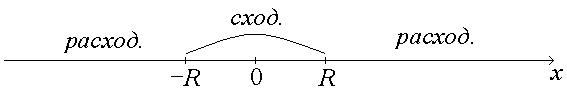
При х = ± R ряд может сходиться или расходиться. Нужна проверка.
Интервал (− R, R) − интервал сходимости степенного ряда; R − радиус сходимости.
Таким образом, областью сходимости степенного ряда является интервал сходимости (без учета проверки точек х = ± R).
Замечание. Интервал сходимости степенного ряда (1) имеет вид (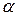 − R;
− R; 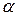 + R).
+ R).
Для определения радиуса сходимости можно использовать признак Даламбера или радикальный признак Коши. Пусть имеется степенной ряд 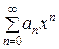 . Рассмотрим ряд, составленный из абсолютных величин его членов
. Рассмотрим ряд, составленный из абсолютных величин его членов 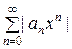 . Для определения сходимости последнего ряда применим признак Даламбера. Пусть существует предел
. Для определения сходимости последнего ряда применим признак Даламбера. Пусть существует предел
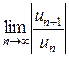 =
= 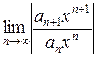 =
= 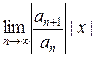 = L | x |.
= L | x |.
Тогда по признаку Даламбера последний ряд 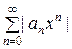 сходится, если L | x | < 1, т.е. если | x | <
сходится, если L | x | < 1, т.е. если | x | < 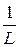 , и расходится, если L | x | > 1, т.е. если | x | >
, и расходится, если L | x | > 1, т.е. если | x | > 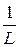 . Обозначим
. Обозначим 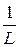 через радиус сходимости R, т.е. R =
через радиус сходимости R, т.е. R = 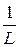 . Тогда
. Тогда
R = 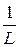 =
= 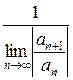 =
= 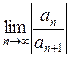 .
.
Таким образом, радиус сходимости степенного ряда 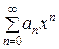 можно определить по формуле
можно определить по формуле
R = 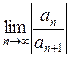 .
.
Аналогично, по радикальному признаку Коши получим
R = 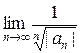 .
.
Пример. Найти область сходимости ряда:
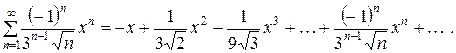
□ Найдем интервал сходимости
Найдем интервал сходимости 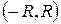 , где R – радиус сходимости. Найдем радиус сходимости R:
, где R – радиус сходимости. Найдем радиус сходимости R:
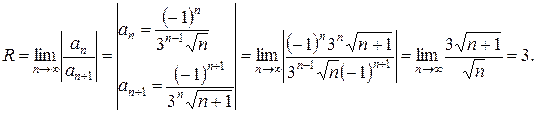
Следовательно, 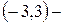 интервал сходимости ряда. Исследуем сходимость ряда на концах интервала:
интервал сходимости ряда. Исследуем сходимость ряда на концах интервала:
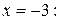
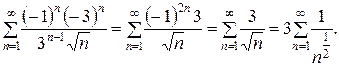
Полученный ряд является обобщенным гармоническим рядом, в котором 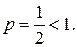 Следовательно, полученный ряд расходится;
Следовательно, полученный ряд расходится;
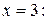
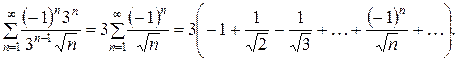
Получили знакочередующийся ряд. Используем теорему Лейбница:
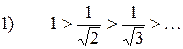
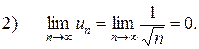
Значит, полученный ряд сходится.
Областью сходимости заданного ряда является промежуток 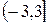 .
.
■
Свойства степенных рядов
10. Если радиус сходимости R степенного ряда 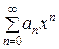 отличен от нуля, то его сумма S (x) непрерывна на интервале сходимости
отличен от нуля, то его сумма S (x) непрерывна на интервале сходимости 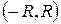 .
.
20. Если для степенного ряда 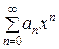 , R
, R 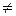 0, то степенной ряд можно почленно дифференцировать на интервале сходимости
0, то степенной ряд можно почленно дифференцировать на интервале сходимости 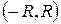 и для его суммы S (x) =
и для его суммы S (x) = 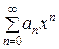 справедливо равенство
справедливо равенство 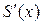 =
= 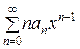 .
.
Следствие. Степенной ряд 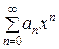 на
на 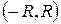 , R
, R 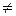 0, можно почленно дифференцировать любое число раз.
0, можно почленно дифференцировать любое число раз.
30. Степенной ряд 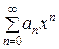 можно почленно интегрировать на любом отрезке [ x 0; x ]
можно почленно интегрировать на любом отрезке [ x 0; x ] 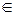 (− R, R), при этом, если S (x) =
(− R, R), при этом, если S (x) = 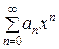 , то
, то
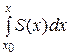 =
= 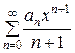 −
−  .
.
Следствие. Степенной ряд 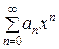 можно почленно интегрировать любое число раз на отрезке [ x 0; x ]
можно почленно интегрировать любое число раз на отрезке [ x 0; x ] 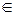 (− R, R).
(− R, R).
40. Операции почленного дифференцирования и интегрирования на любом отрезке [ x 0; x ] 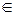 (− R, R) степенного ряд
(− R, R) степенного ряд 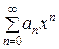 не изменяют его радиуса сходимости R.
не изменяют его радиуса сходимости R.
Ряды Тейлора и Маклорена
Рядом Тейлора для функции f (x) в окрестности точки а называется степенной ряд по степеням х − а вида
f (а) + 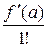 (х − а) +
(х − а) + 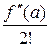 (х − а)2 + … +
(х − а)2 + … + 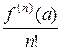 (х − а) п + …. (1)
(х − а) п + …. (1)
Формально ряд Тейлора можно построить для всякой функции, которая в окрестности точки а имеет производные любого порядка. Однако этот ряд будет сходиться к породившей его функции f (x) только при тех значениях х, при которых остаточный член
Rn +1(x) = 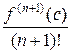 (х − а) п +1
(х − а) п +1
(с = а + 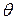 (х − а), 0 <
(х − а), 0 < 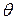 < 1) формулы Тейлора для этой функции стремится к нулю при п → ∞. Если Rn +1(x) → 0 при п → ∞, то можно записать
< 1) формулы Тейлора для этой функции стремится к нулю при п → ∞. Если Rn +1(x) → 0 при п → ∞, то можно записать
f (x) = f (а) + 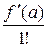 (х − а) +
(х − а) + 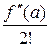 (х − а)2 + … +
(х − а)2 + … + 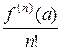 (х − а) п + …,
(х − а) п + …,  (
(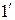 )
)
т.е. записать разложение функции f (x) в ряд Тейлора.
При а = 0 ряд Тейлора есть степенной ряд по степеням х
f (0) + 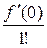 х +
х + 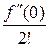 х 2 + … +
х 2 + … + 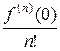 хп +…, (2)
хп +…, (2)
который называется рядом Маклорена.
Тогда разложение функции f (x) в ряд Маклорена имеет вид
f (x) = f (0) + 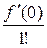 х +
х + 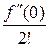 х 2 + … +
х 2 + … + 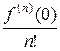 хп + …. (
хп + …. (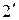 )
)
Для разложения функции f (x) в ряд Тейлора необходимо:
а) написать разложение функции согласно данной формуле;
б) исследовать остаточный член Rn +1(x) формулы Тейлора для данной функции и определить совокупность значений х, при которых 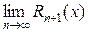 =0.
=0.
Замечание. Для большинства функции область сходимости ряда Тейлора совпадает с совокупностью значений х, при которых 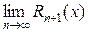 =0. Поэтому при разложении многих функций в ряд Тейлора можно вместо исследования соответствующего остаточного члена Rn +1(x), что во многих случаях весьма затруднительно, исследовать сходимость самого ряда Тейлора как обычного степенного ряда.
=0. Поэтому при разложении многих функций в ряд Тейлора можно вместо исследования соответствующего остаточного члена Rn +1(x), что во многих случаях весьма затруднительно, исследовать сходимость самого ряда Тейлора как обычного степенного ряда.
Пример. Разложить функцию f (x) = 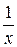 в ряд Тейлора по степеням х − 2.
в ряд Тейлора по степеням х − 2.
□
Из условия видно, что а = 2.
а) Найдем значения этой функции и ее производных для х = а = 2:
f (x) = х −1, f (2) = 2−1;
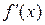 =−1 х −2,
=−1 х −2, 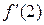 =−1∙2−2;
=−1∙2−2;
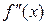 =1∙2 х −3,
=1∙2 х −3, 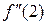 =1∙2∙2−3;
=1∙2∙2−3;
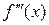 =−1∙2∙3 х −4,
=−1∙2∙3 х −4, 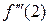 =−1∙2∙3∙2−4;
=−1∙2∙3∙2−4;
…………………………………………………………
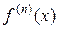 =(−1) пп! х−п −1,
=(−1) пп! х−п −1, 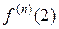 = (−1) пп!2 −п − 1 =
= (−1) пп!2 −п − 1 = 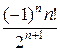 ;
;
…………………………………………………………..
Подставляя в формулу разложения (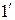 ), получим
), получим
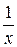 =
=  −
− 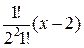 +
+ 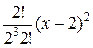 −
− 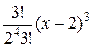 + … +
+ … + 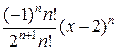 + …
+ …
или
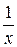 =
=  −
− 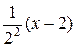 +
+ 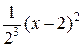 −
− 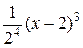 + … +
+ … + 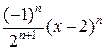 + ….
+ ….
б) Чтобы установить, при каких значениях х полученное разложение справедливо, определим область сходимости построенного ряда.
Найдем радиус сходимости R:
R = 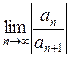 =
= 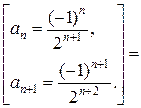
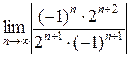 =
= 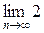 = 2,
= 2,
т.е. интервалом сходимости будет интервал (−2; 2). Но это интервал для х − 2, а не для х. Поэтому проведем следующее преобразование:
−2 < х − 2 < 2, 0 < х < 4,
т.е. интервалом сходимости для построенного ряда будет интервал (0; 4).
Исследуем сходимость ряда на концах интервала.
Пусть х = 0:
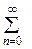
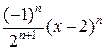 =
= 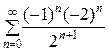 =
= 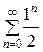 =
= 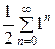 =
=  (1+1+1+..+1+…).
(1+1+1+..+1+…).
Ряд 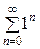 расходится, например, согласно необходимому признаку сходимости.
расходится, например, согласно необходимому признаку сходимости.
Пусть х = 4:
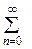
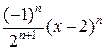 =
=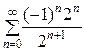 =
=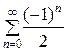 =
= 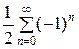 =
=  (1−1+1−...+(−1) п +…).
(1−1+1−...+(−1) п +…).
Ряд 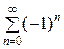 расходится, например, согласно необходимому признаку сходимости.
расходится, например, согласно необходимому признаку сходимости.
Следовательно, областью сходимости построенного ряда является интервал (0; 4). Значит разложение функции f (x)= 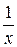 справедливо для всех х
справедливо для всех х 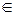 (0; 4).
(0; 4).
■
Разложение элементарных функций в ряд Маклорена
1. Разложить в ряд Маклорена функцию f (x) = 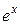 .
.
□
а) Найдем значения этой функции и ее производных:
f (x) = 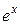 , f (0) =
, f (0) = 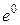 = 1;
= 1;
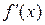 =
= 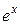 ,
, 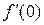 =
= 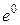 = 1;
= 1;
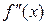 =
= 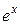 ,
, 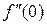 =
= 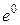 = 1;
= 1;
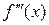 =
= 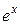 ,
, 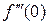 =
= 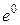 = 1;
= 1;
…………………………………….
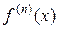 =
= 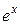 ,
, 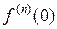 =
= 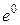 = 1;
= 1;
……………………………………...
Подставляя в формулу разложения (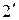 ), получим
), получим
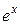 = 1 +
= 1 + 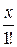 +
+ 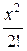 +
+ 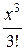 + … +
+ … + 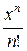 + …. (3)
+ …. (3)
б) Остаточный член формулы Маклорена имеет вид
Rn +1(x) = 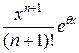 , 0 <
, 0 < 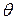 < 1.
< 1.
Чтобы установить, при каких значениях х предел 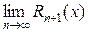 = 0, рассмотрим ряд
= 0, рассмотрим ряд 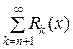 . Применим к этому ряду признак Даламбера:
. Применим к этому ряду признак Даламбера:
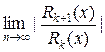 =
= 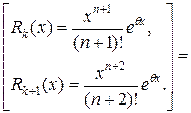
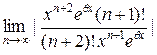 =
= 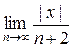 = 0 < 1
= 0 < 1
при любом х.
Следовательно, ряд 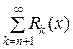 сходится. Отсюда следует, что
сходится. Отсюда следует, что 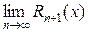 = 0 (необходимый признак сходимости) при любых х. Таким образом, полученный ряд сходится к функции
= 0 (необходимый признак сходимости) при любых х. Таким образом, полученный ряд сходится к функции 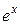 при всех значения х или, другими словами, разложение функции
при всех значения х или, другими словами, разложение функции 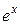 справедливо на интервале (−∞; +∞).
справедливо на интервале (−∞; +∞).
Проверим справедливость разложения по приведенному замечанию, т.е. найдем область сходимости построенного ряда. Найдем радиус сходимости R:
R = 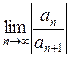 =
= 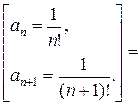
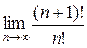 =
= 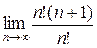 =
=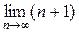 = +∞.
= +∞.
Следовательно, областью сходимости полученного ряда является интервал (−∞; +∞). Делаем вывод, что разложение справедливо для всех х (−∞; +∞).
(−∞; +∞).
■
Аналогично можно разложить в ряд Маклорена следующие функции:
2. f (x) = 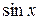 :
:
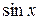 = х −
= х −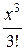 +
+ 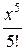 − … + (−1) п
− … + (−1) п 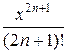 + … (4)
+ … (4)
для х 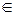 (−∞; +∞).
(−∞; +∞).
3. f (x) = 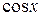 :
:
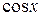 = 1 −
= 1 −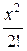 +
+ 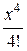 − … + (−1) п
− … + (−1) п 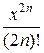 + … (5)
+ … (5)
для х 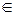 (−∞; +∞).
(−∞; +∞).
4. f (x) = (1+ х) т (биномиальный ряд):
(1+ х) т = 1+ тх +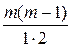 х 2 +
х 2 +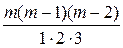 х 3 +…+
х 3 +…+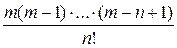 хп +… (6)
хп +… (6)
при т 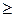 0 для х
0 для х 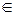 [−1; 1];
[−1; 1];
−1< т < 0 для х 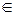 (−1; 1];
(−1; 1];
т 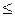 −1 для х
−1 для х 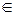 (−1; 1).
(−1; 1).
5. f (x) = 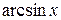 :
:
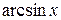 = х +
= х + 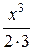 +
+ 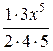 +
+ 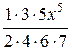 + … +
+ … + 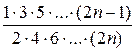 ∙
∙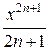 + … (7)
+ … (7)
для х 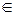 (−1; 1).
(−1; 1).
6. f (x) = 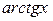 :
:
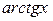 = х −
= х −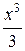 +
+ 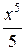 −
− 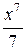 + … + (−1) п
+ … + (−1) п 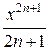 + … (8)
+ … (8)
для х 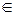 [−1; 1].
[−1; 1].
7. f (x) = 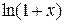 (f (x) =
(f (x) = 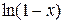 ):
):
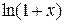 = х −
= х −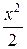 +
+ 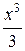 −
− 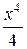 + … + (−1) п
+ … + (−1) п 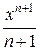 + … (9)
+ … (9)
для х 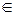 (−1; 1].
(−1; 1].
Заменяя х на − х:
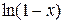 = − х −
= − х −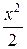 −
− 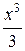 −
− 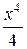 − … −
− … − 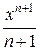 − … (10)
− … (10)
для х 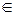 [−1; 1).
[−1; 1).
Приложения степенных рядов
1. Приближенное вычисление значений функций.
В процессе вычислений необходимо помнить, в каждом приближенном результате после запятой должно быть на один знак больше, чем в заданной точности 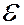 .
.
Пример. Вычислить 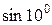 с точностью
с точностью  = 10−5 = 0,00001.
= 10−5 = 0,00001.
□
Воспользуемся разложением функции f (x) = 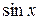 в степенной ряд:
в степенной ряд:
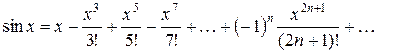 для х
для х 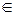 (−∞;+∞).
(−∞;+∞).
Градусную меру измерения необходимо перевести в радианную:
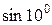 =
= 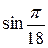 ,
, 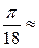 0,174533.
0,174533.
Полагая 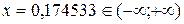 , получим ряд для вычисления
, получим ряд для вычисления 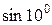 с любой точностью:
с любой точностью:
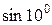 =
= 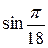 =
= 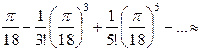 0,174533 − 0,000886 + 0,000001 ≈
0,174533 − 0,000886 + 0,000001 ≈
≈ | 0,000001 <  = 0,00001| ≈ 0,174533 − 0,000886 = 0,173647,
= 0,00001| ≈ 0,174533 − 0,000886 = 0,173647,
т.е. 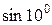 ≈ 0,173647.
≈ 0,173647.
Значения пяти знаков после запятой гарантированы.
■
2. Приближенное вычисление интегралов.
Существуют определенные интегралы, которые не выражаются через элементарные функции. Такие интегралы удобно вычислять с помощью рядов.
Пример. Вычислить определенный интеграл с точностью 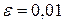 :
:
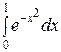 .
.
□ Так как
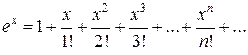 , для х
, для х 
 ,
,
то
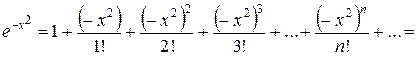
= 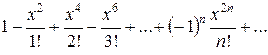 ,
,
для х 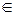
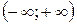 .
.
Подставляя полученное разложение вместо подынтегральной функции, получим:
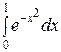 =
= 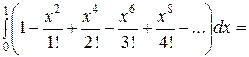
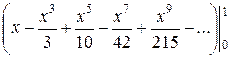 ≈
≈
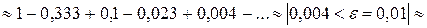
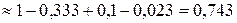 ,
,
т.е.
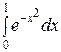 ≈ 0,743.
≈ 0,743.
Значения двух знаков после запятой гарантированы.
■
3. Интегрирование дифференциальных уравнений.
Степенные ряды могут применяться также для решения дифференциальных уравнений, например, в случае, если их решения не удается найти в элементарных функциях.
Так, если требуется решить для уравнения 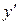 = f (x, y) задачу Коши при начальном условии у (х 0) = у 0, то можно воспользоваться рядом Тейлора
= f (x, y) задачу Коши при начальном условии у (х 0) = у 0, то можно воспользоваться рядом Тейлора
у = 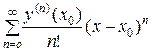 = у (х 0) +
= у (х 0) + 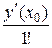 (х − х 0) +
(х − х 0) + 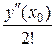 (х − х 0)2 + …,
(х − х 0)2 + …,
где у (х 0) = у 0, 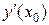 = f (х 0, у 0). Дальнейшие производные
= f (х 0, у 0). Дальнейшие производные 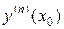 находят последовательным дифференцированием исходного уравнения и подстановкой в результат дифференцирования вместо х, у,
находят последовательным дифференцированием исходного уравнения и подстановкой в результат дифференцирования вместо х, у,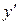 , … значений х 0, у 0,
, … значений х 0, у 0, 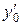 , ….
, ….
Если х 0 = 0, то для решения используют ряд Маклорена:
у = 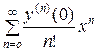 = у (0) +
= у (0) + 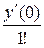 х +
х + 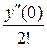 х 2 + ….
х 2 + ….
Аналогично с помощью этих рядов можно интегрировать и уравнения высших порядков.
Пример. Найти три первых, отличных от нуля, члена ряда, определяющего решение дифференциального уравнения с заданными начальными условиями
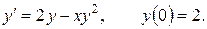
□ Так как х 0 = 0, то воспользуемся разложением
у = 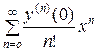 = у (0) +
= у (0) + 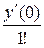 х +
х + 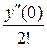 х 2 + ….
х 2 + ….
Найдем коэффициенты при х:
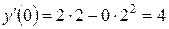 ;
;
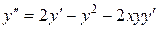 ,
,
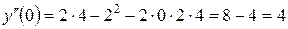 .
.
Подставляя найденные значения в формулу, получим
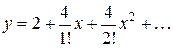
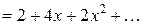 .
.
■
 2014-02-09
2014-02-09 3390
3390