Основным уравнением классической химической термодинамики является фундаментальные соотношения (уравнения) Гиббса, которые определяют связь основных функций состояния (U или S), являющихся экстенсивными величинами, с экстенсивными независимыми переменными. Эти уравнения являются характеристическими функциями, содержат все термодинамические сведения о данной системе и полностью описывают ее состояние. При отсутствии силовых полей для многокомпонентных систем (k – число компонентов) в равновесном состоянии фундаментальные уравнения Гиббса записываются в энергетическом и энтропийном выражениях, соответственно, как функции k+2 независимых экстенсивных переменных U=U(S,V,N1,…,Nk) или S=S(U,V,N1,…,Nk), где V – объем системы Ni – число молекул или молей i -го компонента.В классической химической термодинамике преимущественно используется фундаментальное уравнение Гиббса в энергетическое выражении, а в современной термодинамике неравновесных процессов иногда используется энтропийная форма фундаментального уравнения Гиббса.
|
|
|
Фундаментальные уравнения Гиббса вытекают из обобщения 1-го (dU=dQ-dW+dUвещв) и2-го (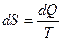 ) законов термодинамики (см. уравнения 1 и 2) и в интегральной и дифференциальной формах при отсутствии внешних полей имеют, соответственно, вид:
) законов термодинамики (см. уравнения 1 и 2) и в интегральной и дифференциальной формах при отсутствии внешних полей имеют, соответственно, вид:
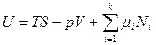 и
и 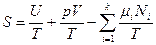 ; (3а)
; (3а)
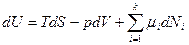 и
и 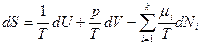 , (3б)
, (3б)
где Т, р, μi – интенсивные параметры состояния (температура, давление, химический потенциал i -го компонента соответственно), не зависящие от размера (объема, массы) системы и в равновесном состоянии одинаковые во всех ее частях. При этом, как уже указывалось выше, при выборе в качестве основной функции состояния внутренней энергии U энтропия S является независимой переменной и, наоборот, при выборе в качестве основной функции состояния энтропии S внутренняя энергия U является независимой переменной.
В уравнениях 3а и 3б интенсивные параметры состояния Т, р, μi являются частными производными основных функций состояния по независимым экстенсивным переменным: для внутренней энергии - соответственно по S, V и N, а для энтропии – по U, V и N. Это следует из того, чтофундаментальное уравнение Гиббса в общем виде является гомогенной функцией многих переменных типа 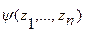 , которая удовлетворяет уравнению
, которая удовлетворяет уравнению 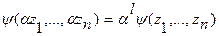 , где l – степень порядка гомогенной функции (положительное целое число). Теорема Эйлера дает определение гомогенной функции l порядка как сумму ее частных производных по независимым переменным в виде соотношения:
, где l – степень порядка гомогенной функции (положительное целое число). Теорема Эйлера дает определение гомогенной функции l порядка как сумму ее частных производных по независимым переменным в виде соотношения: 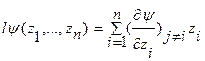 .
.
Дифференциал этой функции имеет вид: 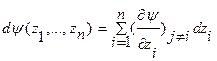 В соответствие с теоремой Эйлера фундаментальные уравнения Гиббса как гомогенные функции 1-й степени (l =1) многих переменных U=U(S,V,N1,…,Nk) и S=S(U,V,N1,…,Nk) в энергетическом и энтропийном выражении записываются в интегральной и дифференциальной формах следующим образом:
В соответствие с теоремой Эйлера фундаментальные уравнения Гиббса как гомогенные функции 1-й степени (l =1) многих переменных U=U(S,V,N1,…,Nk) и S=S(U,V,N1,…,Nk) в энергетическом и энтропийном выражении записываются в интегральной и дифференциальной формах следующим образом:
|
|
|
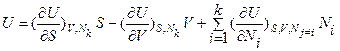 ; (4а)
; (4а) 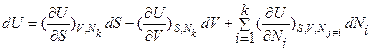 ; (4б)
; (4б)
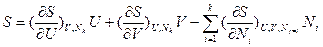 ; (4в)
; (4в)
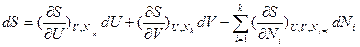 (4г)
(4г)
Отсюда следует, что первые частные производные функций состояния U и S по экстенсивным независимым переменным дают измеряемые и регулируемые интенсивные параметры: 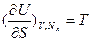 ;
; 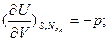
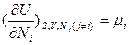 (в энергетическом выражении) и
(в энергетическом выражении) и 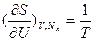 ;
; 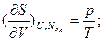
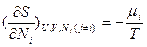 (в энтропийном выражении). Их вторые частные производные дают дополнительные измеряемые параметры (подробнее см. Соотношения Максвелла).
(в энтропийном выражении). Их вторые частные производные дают дополнительные измеряемые параметры (подробнее см. Соотношения Максвелла).
Для имеющей важное практическое значение в современной термодинамике функции S=S(Т,V, Nk), но не являющейся характеристической, частные производные дают следующие соотношения:
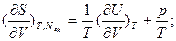
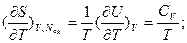
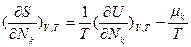 .
.
Если все экстенсивные переменные фундаментального уравнения Гиббса (для U - S, V и N, а для S - U, V и N) обозначить в обобщенном виде через Xi, а интенсивные параметры, являющиеся частными производными внутренней энергии или энтропии, которые обозначены как Y, по экстенсивным параметрам – через 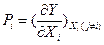 , то фундаментальное уравнение Гиббса может быть записано в обобщенной интегральной форме для k-компонентной системы Y(Х1, …, Хr) в виде:
, то фундаментальное уравнение Гиббса может быть записано в обобщенной интегральной форме для k-компонентной системы Y(Х1, …, Хr) в виде: 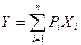 , где n – число экстенсивных параметров в фундаментальном уравнении, причем n ≥ k+2. В дифференциальной форме обобщенное уравнение имеет вид:
, где n – число экстенсивных параметров в фундаментальном уравнении, причем n ≥ k+2. В дифференциальной форме обобщенное уравнение имеет вид: 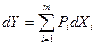 . Соответствующие интенсивные (Pi) и экстенсивные (Xi) параметры фундаментального уравнения считаются сопряженными. При этом еще раз следует напомнить, что при выборе в качестве основной функции состояния внутренней энергии U энтропия S является ее независимой переменной и, наоборот, при выборе в качестве основной функции состояния энтропии S внутренняя энергия U является ее независимой переменной.
. Соответствующие интенсивные (Pi) и экстенсивные (Xi) параметры фундаментального уравнения считаются сопряженными. При этом еще раз следует напомнить, что при выборе в качестве основной функции состояния внутренней энергии U энтропия S является ее независимой переменной и, наоборот, при выборе в качестве основной функции состояния энтропии S внутренняя энергия U является ее независимой переменной.
У равнения, связывающие интенсивные и экстенсивные переменные фундаментального уравнения Pi(X1,…,Xn), являются уравнениями состояния, как например, классическое уравнение состояния веществ, связывающее температуру Т и давление р с объемом V и числом молей N. У равнения состояния представляют собой однородные гомогенные функции нулевой степени, т.е. l=0 и 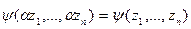 , которые не являются независимыми друг от друга, так как между интенсивными переменными фундаментального уравнения имеется дополнительное соотношение:
, которые не являются независимыми друг от друга, так как между интенсивными переменными фундаментального уравнения имеется дополнительное соотношение: 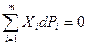 , называемое уравнением Гиббса-Дюгема. Это уравнение получается при вычитании дифференциальной формы фундаментального уравнения из общего дифференциала интегрального фундаментального уравнения по всем его компонентам. При записи фундаментального уравнения в энергетическом выражении в дифференциальной форме:
, называемое уравнением Гиббса-Дюгема. Это уравнение получается при вычитании дифференциальной формы фундаментального уравнения из общего дифференциала интегрального фундаментального уравнения по всем его компонентам. При записи фундаментального уравнения в энергетическом выражении в дифференциальной форме:
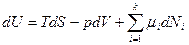 и
и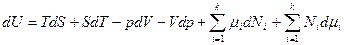 полученные уравнения аналогичны, если
полученные уравнения аналогичны, если 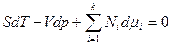 , что и является уравнением Гиббса-Дюгема. При использовании фундаментального уравнения Гиббса в энтропийной форме уравнение Гиббса-Дюгема имеет вид:
, что и является уравнением Гиббса-Дюгема. При использовании фундаментального уравнения Гиббса в энтропийной форме уравнение Гиббса-Дюгема имеет вид: 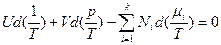 . В обоих формах оно находит важное практическое применение при описании равновесий в многокомпонентных системах. Так, для изобарно-изотермических условий и энергетической формы фундаментального уравнения Гиббса уравнение Гиббса-Дюгема принимает простой вид:
. В обоих формах оно находит важное практическое применение при описании равновесий в многокомпонентных системах. Так, для изобарно-изотермических условий и энергетической формы фундаментального уравнения Гиббса уравнение Гиббса-Дюгема принимает простой вид: 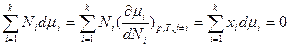 . Оно показывает, что изменение химического потенциала одного из компонентов влияет на изменение химического потенциала других компонентов.
. Оно показывает, что изменение химического потенциала одного из компонентов влияет на изменение химического потенциала других компонентов.
 2014-02-09
2014-02-09 5090
5090








