Основные типы термодинамических потенциалов
С учетом того, что внутренняя энергия и энтропия, наряду с общими свойствами экстенсивных параметров, обладают еще и особыми индивидуальными свойствами, вытекающими из законов термодинамики, вышеприведенное обобщенное определение термодинамических потенциалов позволяет в явном виде определить два наиболее важные с практической точки зрения термодинамических потенциала – свободные энергии Гельмгольца и Гиббса, являющиеся характеристическими функциями состояния.
Свободная энергия Гельмгольца F(Т,V,Nk), как результат преобразования Лежандра функции U(S,V,Nk), в которой S заменена соответствующей частной производной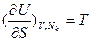 , является характеристической функцией одного интенсивного (Т) и двух экстенсивных (V,Nk) параметров, и в соответствии с обобщенным определением термодинамического потенциала в интегральной (
, является характеристической функцией одного интенсивного (Т) и двух экстенсивных (V,Nk) параметров, и в соответствии с обобщенным определением термодинамического потенциала в интегральной (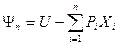 ) и дифференциальной (
) и дифференциальной (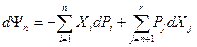 ) форме для многокомпонентной системы определяется следующим образом: F(T,V,N)=U-TS=-TS-PV+
) форме для многокомпонентной системы определяется следующим образом: F(T,V,N)=U-TS=-TS-PV+ 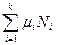 и
и 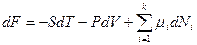 . Первые частные производные F по интенсивным параметрам дают экстенсивные параметры:
. Первые частные производные F по интенсивным параметрам дают экстенсивные параметры: 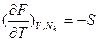 , а по экстенсивным – интенсивные:
, а по экстенсивным – интенсивные: 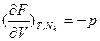 (термическое уравнение состояния),
(термическое уравнение состояния), 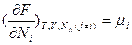 . В закрытых системах уменьшение свободной энергии Гельмгольца равно работе, совершенной системой в изотермическом обратимом процессе. Как термодинамический потенциал свободная энергия Гельмгольца очень полезна при контролируемом объеме, т.е. в газообразных системах, а также при расчетах методами статистической термодинамики: F=-kBlnZ, где kB – константа Больцмана, Z - статистическая сумма (интеграл) по состояниям.
. В закрытых системах уменьшение свободной энергии Гельмгольца равно работе, совершенной системой в изотермическом обратимом процессе. Как термодинамический потенциал свободная энергия Гельмгольца очень полезна при контролируемом объеме, т.е. в газообразных системах, а также при расчетах методами статистической термодинамики: F=-kBlnZ, где kB – константа Больцмана, Z - статистическая сумма (интеграл) по состояниям.
Б. Свободная энергия Гиббса и химический потенциал.
Свободная энергия Гиббса G(T,р,Nk), как результат преобразования Лежандра функции U(S,V,Nk), в которой S и V заменены соответствующими частными производными 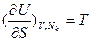 и
и 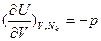 , является характеристической функцией двух интенсивных (Т и р) и одного экстенсивного (Nk) параметров и в соответствии с обобщенным определением термодинамического потенциала в интегральной (
, является характеристической функцией двух интенсивных (Т и р) и одного экстенсивного (Nk) параметров и в соответствии с обобщенным определением термодинамического потенциала в интегральной (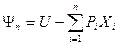 ) и дифференциальной (
) и дифференциальной (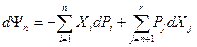 ) форме определяется для многокомпонентных систем следующим образом: G(T,p,N)=U+pV-TS= -TS+pV+
) форме определяется для многокомпонентных систем следующим образом: G(T,p,N)=U+pV-TS= -TS+pV+ 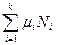 и
и 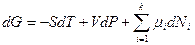 . Для закрытых систем уменьшение свободной энергии Гиббса равно работе, совершенной системой в изобарно-изотермическом обратимом процессе. Ее частные производные:
. Для закрытых систем уменьшение свободной энергии Гиббса равно работе, совершенной системой в изобарно-изотермическом обратимом процессе. Ее частные производные: 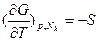 ,
,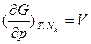 (термическое уравнение состояния) и
(термическое уравнение состояния) и 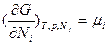 - химический потенциал, равный для однокомпонентных систем мольной свободной энергии Гиббса. Свободная энергия Гиббса и химический потенциал из всех термодинамических потенциалов находят наиболее широкое практическое применение при описании конденсированных систем, так как все независимые переменные в них (интенсивные р и Т, а также экстенсивный параметр - число молей компонентов Ni) легко измеряются и контролируются. Функция G (Т,р,Nk) часто используется в классической химической термодинамике в виде средней мольной величины:
- химический потенциал, равный для однокомпонентных систем мольной свободной энергии Гиббса. Свободная энергия Гиббса и химический потенциал из всех термодинамических потенциалов находят наиболее широкое практическое применение при описании конденсированных систем, так как все независимые переменные в них (интенсивные р и Т, а также экстенсивный параметр - число молей компонентов Ni) легко измеряются и контролируются. Функция G (Т,р,Nk) часто используется в классической химической термодинамике в виде средней мольной величины: 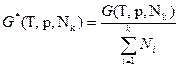 , которая в дифференциальной форме записывается как функция мольных долей компонентов хi:
, которая в дифференциальной форме записывается как функция мольных долей компонентов хi: 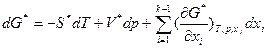 . Последнее уравнение формально аналогично уравнению для dG, выведенное из обобщенного определения G:
. Последнее уравнение формально аналогично уравнению для dG, выведенное из обобщенного определения G: 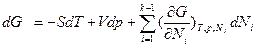 . Следовательно, средняя мольная величина G* является характеристической функцией, т.е. она содержит все термодинамические сведения о данной системе. Так, ее частные производные по интенсивным параметрам (р, Т) дают среднюю мольную энтропию и средний мольный объем:
. Следовательно, средняя мольная величина G* является характеристической функцией, т.е. она содержит все термодинамические сведения о данной системе. Так, ее частные производные по интенсивным параметрам (р, Т) дают среднюю мольную энтропию и средний мольный объем: 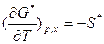 ,
,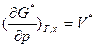 . Однако, частная производная средней мольной величины G* по мольной доле компонентов
. Однако, частная производная средней мольной величины G* по мольной доле компонентов 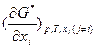 не является химическим потенциалом, в отличие от частного производного свободной энергии Гиббса G (Т,р,Nk) по числу молей компонентов:
не является химическим потенциалом, в отличие от частного производного свободной энергии Гиббса G (Т,р,Nk) по числу молей компонентов: 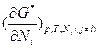 , которое является химическим потенциалом компонентов
, которое является химическим потенциалом компонентов 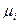 . При этом
. При этом 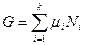 , а
, а 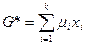 .
.
Химический потенциал как парциальная мольная 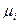 (для многокомпонентных систем) или просто мольная g (для однокомпонентных систем) свободная энергия Гиббса связан с температурой и парциальными мольными величинами функций состояния S и H:
(для многокомпонентных систем) или просто мольная g (для однокомпонентных систем) свободная энергия Гиббса связан с температурой и парциальными мольными величинами функций состояния S и H: 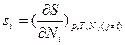 и
и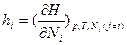 аналогичными соотношениями:
аналогичными соотношениями: 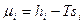 ;
; 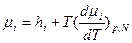 .
.
Уравнение Гиббса-Дюгема с использованием частных производных как свободной энергии Гиббса G, таки ее средней мольной величины G* по интенсивным переменным, а также частных производных химического потенциала по числу молей и мольным долям формально имеет аналогичный вид для общих и изобарно-изотермических условий или процессов соответственно:
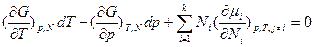 и
и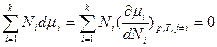 ;;
;; 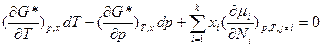 и
и 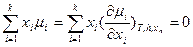 .
.
 2014-02-09
2014-02-09 1808
1808
