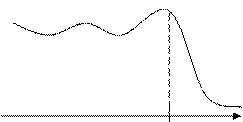
Периодический прямоугольный потенциал (решение Кронинга-Пенни).
| Рис. | Найдём решение уравнения Шредингера для потенциала, показанного на рис. …. Волновая функция имеет вид |
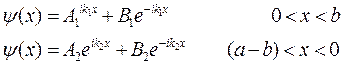
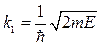
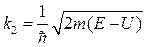
Из условия непрерывности волновой функции и её производной при x=0 получаем
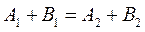
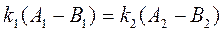
Кроме того, волновая функция должна удовлетворять условию
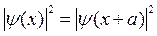
из которого следует, что значение волновой функции в соответствующих точках, отличающихся на величину, кратную периоду потенциала, может отличаться только фазовым множителем
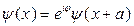 (*)
(*)
Подставляя в (*) соответствующие выражения для 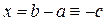 волновых функций в точках
волновых функций в точках 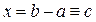 и
и 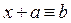 , а также в производную от (x) получим следующие уравнения:
, а также в производную от (x) получим следующие уравнения:
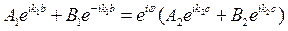
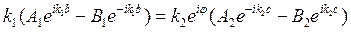
Совместное решение уравнений (*) и (**) приводит к следующему соотношению:
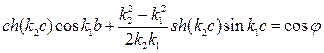
Так как k1 и k2 выражаются через E согласно (), то уравнение позволяет в принципе найти спектр значений энергии как функуию произвольного параметра φ. Для более наглядного анализа уравнения () воспользуемся следующим приёмом. Введём величину 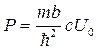 , которая характеризует прозрачность барьера, и найдём вид уранения () при с → 0, U0 → ∞ при условии, что P = const. После этих преобразований приходим к выражению:
, которая характеризует прозрачность барьера, и найдём вид уранения () при с → 0, U0 → ∞ при условии, что P = const. После этих преобразований приходим к выражению:
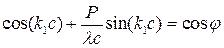
Графическое решение этого уравнения показано на рис.
Градиент вблизи поверхности
х | Вблизи поверхности изменяются плотность, длины связей, упругость связей, ориентация молекул, …, проводимость, коэффициент преломления света и т.д. Поверхностная энергия |
Доля поверхности как функция размера
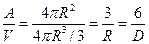
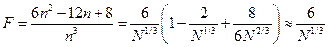
X-ray Дифракция на наночастицах
Ширина пика дифракции определяется
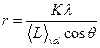
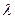 - длина волны,
- длина волны, 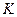 - константа Шерера, зависит от формы частиц (напр. Равна 0,9 для сферических).
- константа Шерера, зависит от формы частиц (напр. Равна 0,9 для сферических).
 |
Для сферических частиц 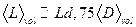
В малых частицах происходит “сжатие” постоянной кристаллической решётки.
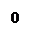 |

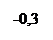 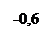 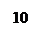 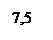 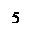 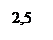 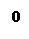 | 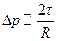 Лапласовское давление Если Лапласовское давление Если 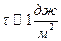 , то , то 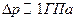 для для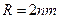 |

 2014-02-09
2014-02-09 731
731