2014-02-09
639
Теперь рассмотрим обратимую мономолекулярную реакцию АÛВ, для которой k1 и k2 – константы скорости прямого и обратного процессов. Соответствующие дифференциальные уравнения для функции распределения и производящей функции имеют вид:
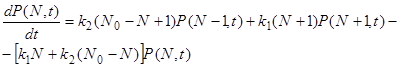(18)
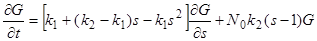(19)
Если начальное состояние системы NA = N0, NB =0, то решение (19) будет
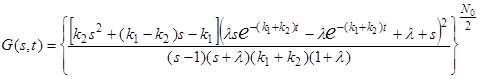(20)
Отсюда по формулам (11) и (12) находим
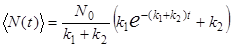(21)
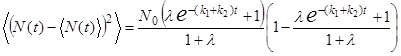(22)
где l = k1 / k2 – обратная константа равновесия химической реакции. При l ®¥ формулы (21) и (22) переходят в (11) и (12) соответственно, что отвечает предельному случаю необратимого процесса.
3.3. Бимолекулярная реакция 2А®В.
Нахождение точного стохастического решения для бимолекулярного химического процесса является намного более сложной задачей. Рассмотрим, например, необратимую химическую реакцию 2А®В, характеризующуюся константой скорости k. В рамках традиционной химической кинетики имеем дифференциальное уравнение для средней концентрации [ A ] в виде
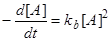(23)
решение которого есть
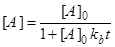(24)
где [ A ]0 – начальная концентрация, а kb – константа скорости бимолекулярной химической реакции. Применение этого подхода к малой системе, в которой содержится небольшое число молекул реагента, будет завышать скорость реакции. Например, при NA =1 скорость реакции должна быть равна нулю, в то время как в соответствии с уравнением (23) она имеет конечное ненулевое значение. С учетом этого обстоятельства можно ввести поправку, записав уравнение (23) в следующем модифицированном виде:
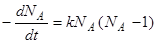(25)
Здесь k – вероятность реакции, отнесенная к единице времени, для произвольной пары молекул. Поэтому скорость реакции будет пропорциональна числу различных пар молекул, которые можно составить из их общего числа N.
Тогда, решая уравнение (25) и затем переходя от числа молекул к концентрациям, получим следующую зависимость:
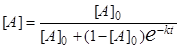(26)
Это – так называемое модифицированное кинетическое уравнение. Однако оно не учитывает флуктуации числа молекул и поэтому при малых значениях N будет давать отклонения от истинной кинетики процесса.
Стохастический подход приводит к следующим уравнениям для функции распределения и производящей функции:
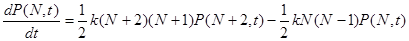(27)
и
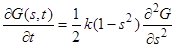(28)
Решение уравнения (28) находится в виде бесконечного ряда
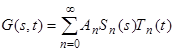(29)
где
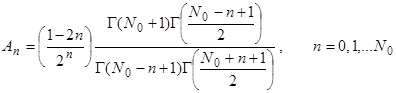(30)
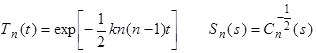(31)
G(n) – гамма-функция, а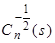 
- многочлен Гегенбауэра. Также можно найти среднее значение числа молекул и второй факториальный момент функции распределения.
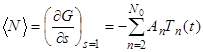(32)
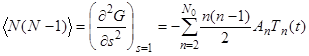(33)
На рис. показаны расчетные кривые для N0 =10 для всех трех рассмотренных выше кинетических подходов. Видно, что детерминированное кинетическое описание занижает скорость реакции относительно истинного стохастического описания, а модифицированное кинетическое описание завышает скорость реакции.
3.4. Реакция А+В®С.
Обозначим через N число молекул А в момент времени t, а через N0 и М0 – число молекул А и В в начальный момент времени соответственно. Тогда М0 – N0 - N будет число молекул В в момент времени t. Без ограничения общности можно считать, что М0 – N0 ³0. Соответствующие дифференциальные уравнения для функции распределения P (N, t) и ее производящей функции имеют вид:
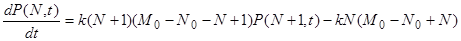(34)
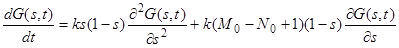(35)
Применяя метод разделения переменных, представляем решение уравнения (35) в виде
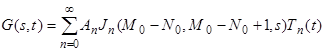(36)
где Jn (p, q, s) – полиномы Якоби, Tn (t)=exp[- n (n + M0 - N0) kt ] и
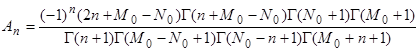(37)
Выражения для первого и второго факториального момента функции распределения имеют вид:
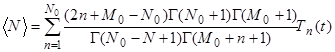(38)
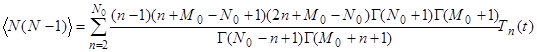(39)
В частном случае реакции псевдо-первого порядка, когда M0 >> N0, можно ограничиться только первым членом ряда в формулах (38) и (39), и эти выражения будут иметь вид:
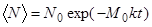(40)
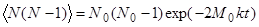(41)
Относительной мерой флуктуаций является коэффициент вариации
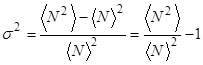(42)
На рис. показана зависимость коэффициента вариации от времени для различных начальных значений числа реагирующих молекул рассматриваемой бимолекулярной реакции А+В®С при эквимолярном соотношении реагирующих веществ. Эти зависимости рассчитаны численно по формулам (38), (39) и (42).
