Свойства функций, имеющих предел

Теорема 1. Если функция имеет предел в точке, то этот предел единственный.

Теорема 2. Если функция имеет предел в точке, то она ограничена в некоторой проколотой окрестности этой точки.

Теорема 3. Если функция имеет предел 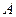в точке , то существует проколотая окрестность точки, в которой функция имеет знак, совпадающий со знаком предела.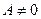

Теорема 4. Если 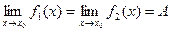и в некоторой проколотой окрестности точки имеют место неравенства 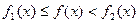, то .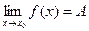

Теорема 5. Пусть функции и 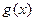имеют предел в точке . Тогда справедливы формулы:

1) 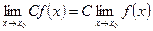, где С=const;

2)

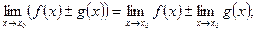
3)

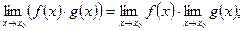
4)

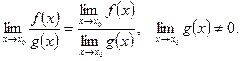
Замечание 1. Формулы суммы и произведения обобщаются на любое конечное число множителей. Если использовать их для бесконечного количества множителей, то может возникнуть ошибка.

Замечание 2. Если в результате применения формул 1) – 4) приходим к выражениям типа

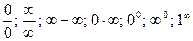
которые называют неопределенностями, то следует вначале устранить неопределенность, сделав тождественные преобразования.