Пусть при.
Замечательные пределы
Следствия: 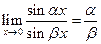 ;
; 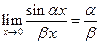 .
.
2. Второй замечательный предел 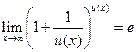 или
или 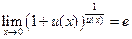 .
.
Следствия: 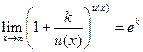 ;
; 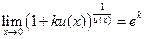 .
.
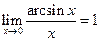 ;
; 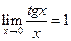 ;
; 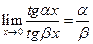 ;
; 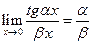 ;
;
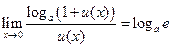 ;
; 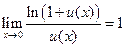 ;
;
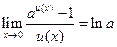 ;
; 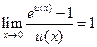 ;
; 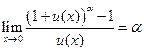 ;
; 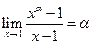
40. Бесконечно малые функции (БМФ)
Определение 1. Функция  - бесконечно малая при
- бесконечно малая при 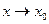 (или
(или 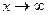 ), если
), если
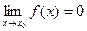 (1)
(1)
Для бесконечно малых функций справедливы следующие теоремы.
Теорема 1. Если 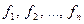 – бесконечно малые функции при
– бесконечно малые функции при 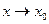 , то бесконечно малыми являются также:
, то бесконечно малыми являются также:
1) 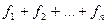 ; (2)
; (2)
2) 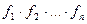 .
.
Доказательство. 1) т.к. функции бесконечно малые, то по определению 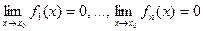 . Рассмотрим предел суммы (2):
. Рассмотрим предел суммы (2):
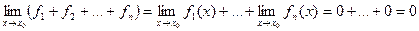 .
.
2) аналогично.
Примечание. Условие теоремы 1 указывает, что количество БМФ произвольное, но конечное. Если рассматривать бесконечное количество функций, то их сумма и произведение уже могут не быть бесконечно малой функцией.
Теорема 2. Произведение бесконечно малой функции  при
при 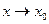 и ограниченной функции
и ограниченной функции 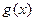 является бесконечно малой функцией при
является бесконечно малой функцией при 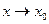 .
.
Теорема 3. Для того, чтобы число А было пределом функции  в точке
в точке  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
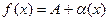 , (3)
, (3)
где 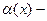 бесконечно малая функция при
бесконечно малая функция при 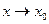 .
.
Доказательство. I. Необходимость. Пусть 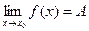 . Докажем, что выполняется равенство (3). Обозначим
. Докажем, что выполняется равенство (3). Обозначим
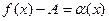 (4)
(4)
Докажем, что 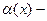 бесконечно малая функция при
бесконечно малая функция при 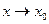 . Вычислим предел
. Вычислим предел
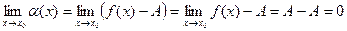 .
.
Доказали, что 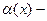 БМФ. Из (4) получаем (3).
БМФ. Из (4) получаем (3).
II. Достаточность. Допустим, что выполняется равенство (3). Докажем, что в таком случае 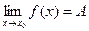 .
.
Вычислим предел:
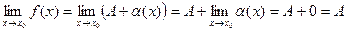 .
.
 2014-02-09
2014-02-09 1580
1580
