Тема 1. Предел функции
Раздел: Предел и непрерывность функции
Допустим, что функция  определена в некоторой области
определена в некоторой области 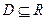 . Будем рассматривать понятие предела функции
. Будем рассматривать понятие предела функции  в точке
в точке  .
.
Можно дать определение функции в точке по Гейне (см. конспект1-го курса) и по Коши.
Определение 1 (по Гейне). Число 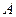 называется пределом функции
называется пределом функции  в точке
в точке  , если функция
, если функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  (за исключением, может быть, самой точки
(за исключением, может быть, самой точки  ), и для всякой последовательности
), и для всякой последовательности 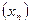 из окрестности
из окрестности  и
и 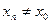 , последовательность соответствующих значений функции сходится к числу
, последовательность соответствующих значений функции сходится к числу 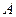 , т.е.
, т.е. 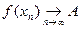 .
.
Записывают
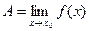 .
.
Определение 2 (по Коши). Число А называется пределом функции  в точке
в точке  , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа 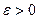 найдется такое число
найдется такое число 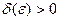 , что для всех таких
, что для всех таких 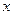 , что
, что
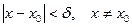 (1)
(1)
выполняется неравенство
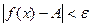 . (2)
. (2)
Заметим, что число 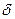 выбирается как «своё» (по значению) для каждой точки
выбирается как «своё» (по значению) для каждой точки  и для каждого
и для каждого 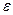 , т.е.
, т.е. 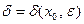 .
.
Первое определение называется также определением предела функции «на языке последовательностей», а второе – определением предела «на языке 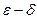 » (эпсилон-дельта).
» (эпсилон-дельта).
Определение 2 можно дать в геометрической форме. Используя свойство модуля неравенство (1) можно записать в виде
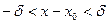 , т.е.
, т.е.
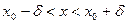 ,
,
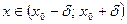 .
.
Аналогично из (2) 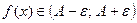 .
.
Определение 3 (геометрическая форма определения Коши). Число А – предел функции  в точке
в точке  , если функция
, если функция  определена в некоторой проколотой окрестности точки
определена в некоторой проколотой окрестности точки  и если для всякой
и если для всякой 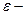 окрестности точки А существует проколотая
окрестности точки А существует проколотая 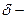 окрестность точки
окрестность точки  такая, что как только аргумент
такая, что как только аргумент  принадлежит этой проколотой
принадлежит этой проколотой 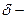 окрестности, то значение функции принадлежит
окрестности, то значение функции принадлежит 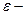 окрестности точки А.
окрестности точки А.
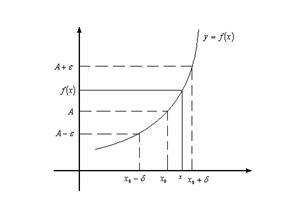
Дадим графическую иллюстрацию этого определения.
Для того, чтобы доказать графически, что число А является пределом функции в точке  , необходимо выбрать произвольную
, необходимо выбрать произвольную 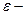 окрестность точки А, т.е. интервал с центром в точке А длины
окрестность точки А, т.е. интервал с центром в точке А длины 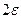 , который лежит на оси
, который лежит на оси 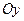 . Для каждого произвольного
. Для каждого произвольного 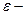 интервала доказать, что существует
интервала доказать, что существует 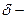 интервал точки
интервал точки  на оси
на оси 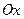 , что как только рассматривает аргументы из этого интервала, то соответствующие значения функции попадают в
, что как только рассматривает аргументы из этого интервала, то соответствующие значения функции попадают в 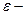 интервал точки А.
интервал точки А.
Можно доказать эквивалентность определений предела по Коши и по Гейне.
Не всякая функция имеет предел в точке. Например, функция 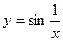 в точке
в точке 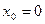 предела не имеет. В этой точке он неопределен вообще. Не имеет предела в точке
предела не имеет. В этой точке он неопределен вообще. Не имеет предела в точке 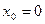 функция
функция 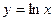 . По определению предела это должно быть число. Функция
. По определению предела это должно быть число. Функция 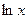 при
при 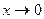 не стремится к конечному числу.
не стремится к конечному числу.
Т.о. относительно предела функции в точке возможны следующие случаи:
I. Функция имеет предел в точке. Это число.
II. Функция не имеет предела в точке:
1) она является бесконечно большой в этой точке, и хотя предела в этом случае нет, записывают
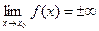 .
.
2) Предел не определен вообще и не ясно, к чему стремится функция в данной точке.
Кроме определения предела в точке рассматривают предел функции на бесконечности, т.е. при  . В этом случае
. В этом случае 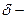 окрестностью называется множество точек
окрестностью называется множество точек 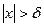 . Относительно предела функции на бесконечности возможны следующие случаи:
. Относительно предела функции на бесконечности возможны следующие случаи:
I. Предел существует, и это число (рис. 1);
II. Предел не существует:
1) 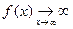 , т.е. функция является бесконечно большой, и записывают
, т.е. функция является бесконечно большой, и записывают 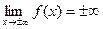 (рис.2);
(рис.2);
2) предел неопределен вообще (рис. 3).
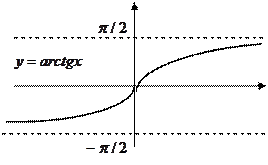
 2014-02-09
2014-02-09 12760
12760
