Эквивалентность бесконечно малых функций

Определение. Функции и 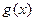, которые определены в окрестности точки , называются эквивалентными при 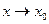, если выполняется

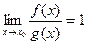. (1)

Обозначается:

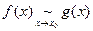(2)

Теорема. Если функции и 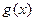эквивалентны при 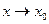, то

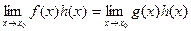. (3)

Доказательство. .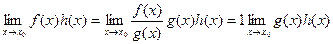

Доказательство теоремы показывает, что под знаком предела можно заменять функцию на эквивалентную ей (более простую) в произведении. Теорема справедлива и когда 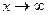для эквивалентных функций на бесконечности.

Особое значение при таком подходе для практики имеют эквивалентности, которые получаем на основе замечательных пределов.