Таблица эквивалентных БМФ
Пусть 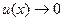 (БМФ) при
(БМФ) при 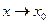 . Тогда верны формулы:
. Тогда верны формулы:
1. 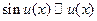 ; 2.
; 2. 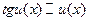 ; 3.
; 3. 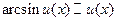 ; 4.
; 4. 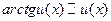 ;
;
5. 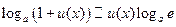 ; 6.
; 6. 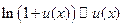 ;
;
7. 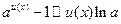 ; 8.
; 8. 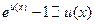 ;
;
9. 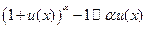 ; 10.
; 10. 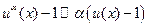 ;
;
11. 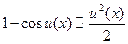 ; 12.
; 12. 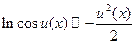 .
.
В качестве предела функции в точке 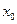 ввели число
ввели число 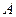 , которое не зависит от способа стремления аргумента
, которое не зависит от способа стремления аргумента 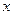 к числу
к числу 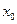 . В определении предела по Гейне было указано, что число
. В определении предела по Гейне было указано, что число 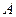 является пределом, если выбирается любая последовательность
является пределом, если выбирается любая последовательность 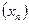 , сходящаяся к
, сходящаяся к 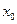 . Рассмотрим следующие ситуации.
. Рассмотрим следующие ситуации.
Определение 1. Если  стремится к пределу
стремится к пределу 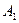 при условии
при условии 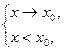 то
то 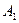 – называется левостороннимпределом функции
– называется левостороннимпределом функции  :
:
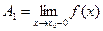 . (1)
. (1)
Определение 2. Если  стремится к пределу
стремится к пределу 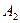 при условии
при условии 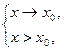 то
то 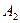 называется правостороннимпределом функции
называется правостороннимпределом функции  :
:
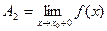 . (2)
. (2)
Левосторонний и правосторонний пределы называются односторонними. Они определяются при ограничении на стремление аргумента к числу 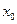 только слева или только справа.
только слева или только справа.
Из определения предела и односторонних пределов приходим к справедливости следующего утверждения:
Если функция  имеет предел в точке
имеет предел в точке 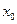 , равный числу
, равный числу 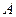 , то она имеет также односторонние пределы в этой точке, равные
, то она имеет также односторонние пределы в этой точке, равные 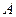 , т.е.
, т.е.
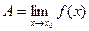
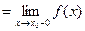
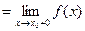 .
.
Можно доказать обратное утверждение.
Теорема. Если функция  имеет в точке
имеет в точке 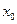 равные односторонние пределы, равные числу
равные односторонние пределы, равные числу 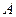 , то в этой точке она также имеет предел, равный числу
, то в этой точке она также имеет предел, равный числу 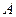 .
.
Если односторонние пределы рассматривать в точке 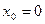 , то их обозначают
, то их обозначают
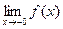 и
и 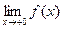 .
.
 2014-02-09
2014-02-09 1107
1107








