Доказательство

Пример 1.6.

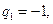
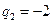
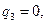
Пусть 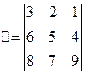. Построить .

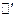Проверить, что .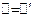

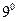Теорема 1.3 (аннулирования).

Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.

Докажем к примеру, что сумма произведений элементов второго столбца на соответствующие алгебраические дополнения элементов первого столбца равна нулю. Пусть задан определитель (1.5). Тогда имеем разложение (1.6)

.

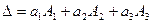Алгебраические дополнения 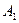, , 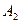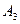не зависят от самих элементов 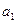, , 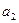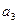. Поэтому если в обеих частях равенства (1.6) числа 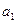, , 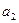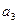заменить произвольными числами 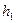, , 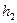, 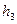то получится верное равенство

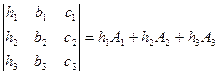(1.10).

Если теперь в равенстве (1.10) в качестве 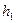, , 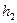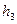взять элементы 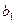, , 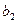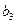второго столбца, то согласно свойству (3) определитель с двумя одинаковыми столбцами равен нулю.