Скалярное произведение векторов

Пусть векторы и 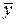принадлежат евклидову пространству.

Скалярное произведение векторов и 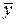обозначается как

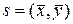, (2.1.30)

т.е. двум векторам и 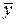ставится в соответствие число .

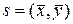В соответствии с данным выше определением евклидового пространства скалярное произведение векторов должно обладать свойствами:

;

;

;

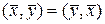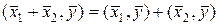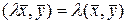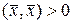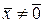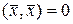, если и , если 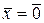. (2.1.31)

Чаще всего скалярное произведение векторов определяется формулой

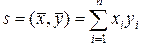. (2.1.32)

Положительно определенной матрицей называется вещественная сим-

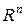метричная матрица, если для любого вектора пространства справедливы соотношения:

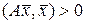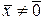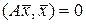, если и , если 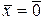. (2.1.33)

Можно показать, что для любой матрицы 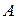справедливо равенство

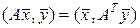. (2.1.34)