Определение матричной нормы эквивалентно определению векторной нормы.
Пусть 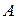 – произвольная вещественная матрица размером
– произвольная вещественная матрица размером 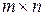 .
.
Функция
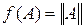
называется нормой вещественной матрицы, если она обладает следующими свойствами:
1) 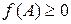 , причем
, причем 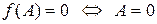 ;
;
2) 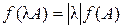 , где
, где 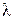 – произвольное вещественное число;
– произвольное вещественное число;
3) 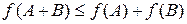 , где
, где  – произвольная вещественная матрица размером
– произвольная вещественная матрица размером 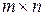 .
.
Чаще всего в вычислительной линейной алгебре используются норма Фробениуса и p-нормы равные соответственно
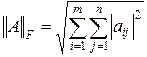 ; (2.1.48)
; (2.1.48)
 . (2.1.49)
. (2.1.49)
Заметим, что все матричные p -нормы определяются через векторные p -нормы, рассмотренные в предыдущем пункте. Вводимая так норма называется индуцированной, поскольку ее конкретный вид зависит от используемой нормы вектора. В частности, можно записать следующие нормы матрицы:
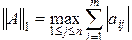 (2.1.50)
(2.1.50)
– максимальная сумма модулей элементов по столбцам;
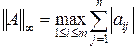 (2.1.51)
(2.1.51)
– максимальная сумма модулей элементов по строкам;
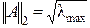 , (2.1.52)
, (2.1.52)
где 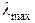 – максимальное собственное число матрицы
– максимальное собственное число матрицы 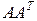 .
.
Для симметричной матрицы порядка 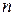 имеем:
имеем:
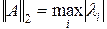 , (2.1.53)
, (2.1.53)
где 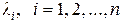 – собственные значения матрицы
– собственные значения матрицы 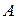 .
.
p -Нормы обладают тем важным свойством, что для каждой вещественной матрицы 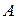 размером
размером 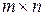 и произвольного вещественного вектора
и произвольного вещественного вектора  n -го порядка выполняется неравенство
n -го порядка выполняется неравенство
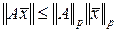 . (2.1.54)
. (2.1.54)
Нормы Фробениуса и p -нормы удовлетворяют определенным неравенствам, часто используемым в матричных вычислениях:
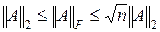 ;
;
 ;
;
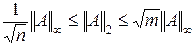 ;
;
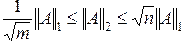 . (2.1.55)
. (2.1.55)
 2014-02-09
2014-02-09 4311
4311







