Норма вектора. Некоторые свойства векторных норм. Абсолютная и относительная погрешности. Сходимость

Некоторым обобщением понятия длины вектора (оценкой величины вектора) является величина, называемая норма вектора. Функция

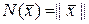
является нормой вектора, если она обладает следующими свойствами:

1) 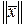³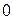 (равенство только при );

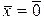2) 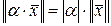; (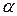– число, – вектор)

3) 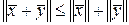– неравенство треугольника.

Чтобы отличить одну норму от другой используются индексы при двойной черте.

Полезный класс векторных норм – это p-нормы, определяемые как

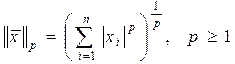. (2.1.35)

Наиболее важными из p -норм являются 1, 2 и 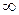нормы:

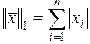(2.1.36)

– норма по модулю (частный случай (2.1.35) при );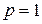

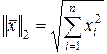(2.1.37)

– «евклидова» норма (частный случай (2.1.35) при );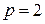

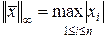(2.1.38)

– максимум модуля для элементов вектора (частный случай (2.1.35) при ).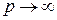

Очевидно, что евклидова норма 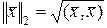. Это соответствует естественному понятию длины вектора в двумерном и трехмерном пространстве.

Единичным вектором по отношению к норме называется вектор , удовлетворяющий равенству .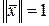

Классический результат о p -нормах – неравенство Гельдера

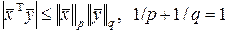. (2.1.39)

Очень важным частным случаем этого неравенства является неравенство Коши-Шварца:

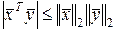. (2.1.40)

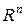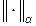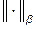Все нормы в эквивалентны, т.е. для двух норм и в 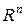существуют положительные константы 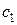и 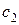, такие, что

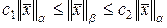(2.1.41)

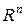для всех из пространства . Например, для вектора из 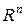имеем:

;

;

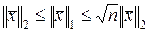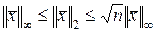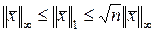. (2.1.42)

В вычислительной математике большую роль играет понятие «близости» двух векторов. Это соответствует понятию «расстояния», определяемому формулой

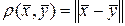, (2.1.43)

т.е. расстояние между векторами равно норме от их разности:

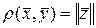, где 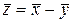. (2.1.44)

Оценка близости двух векторов используется для определения погрешности решения в итерационных методах.

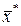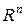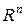Пусть вектор пространства есть приближение к вектору пространства . Для заданной векторной нормы будем говорить, что

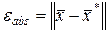(2.1.45)

есть абсолютная погрешность ,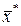

а при 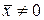формула

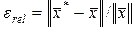(2.1.46)

задает относительную погрешность .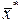

Сходимость. Будем говорить, что последовательность векторов 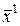, , 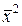…, , … 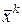сходится к вектору , если

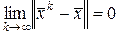. (2.1.47)

Отметим, что вследствие приведенных выше свойств векторных норм сходимость в a -норме влечет сходимость в b -норме и наоборот.