2014-02-09
1165
Из равенства
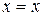
вычитаем сторонами уравнение (2.6.1)
.
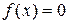Получаем
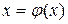, (2.6.15)
где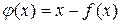 
.
Метод итерации состоит в следующем. Задается начальное приближение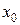 
. Затем последовательно вычисляются 
, 
, …, 
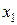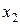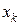, … по формуле
, 
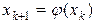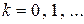. (2.6.16)
Вычисления производятся до тех пор, пока не выполнится условие
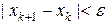, (2.6.17)
после чего приближенное решение принимается равным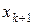 
.
Достаточное условие сходимости метода.
Пусть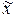 
– корень, 
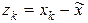– погрешность, тогда (по теореме Лагранжа):
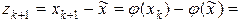
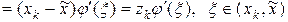
Пусть
.
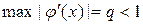Тогда справедлива цепочка неравенств
,
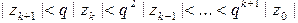откуда следует, что
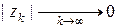т.к. 
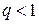и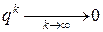 
.
Следовательно, достаточным условием сходимости является
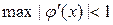. (2.6.18)
Количество итераций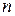 
, достаточное для получения приближенного решения уравнения с заданной точностью 
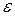определяется из условия 
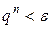. Учитывая, что пр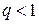и и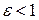 
значения натурального логарифма от этих величин отрицательные (
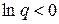и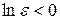 
), получим следующую оценку
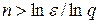. (2.6.19)
Очевидно, что чем сильнее неравенство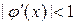 
, т.е. чем меньше 
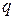, тем меньше количество итераций 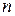, достаточное для получения приближенного решения уравнения с заданной точностью .
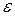Обобщение. Если достаточное условие сходимости итераций (2.6.18) не выполняется, то вместо исходной задачи (2.6.1) можно рассмотреть эквивалентную ей задачу
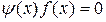, (2.6.20)
где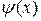 
– некоторая, специально подобранная, знакопостоянная на отрезке 
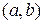, функция.
Тогда в итерационном процессе (2.6.16) функция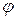 
имеет вид
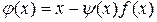. (2.6.21)
Для сходимости так построенного итерационного процесса функция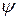 
должна быть подобрана из достаточного условия сходимости (2.6.18).
Рассмотрим два примера метода итерации: метод простой итерации и метод Ньютона.
Метод простой итерации. В итерационном процессе можно, в частности, принять
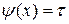, (2.6.22)
где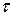 
– специально подобранное число (итерационный параметр).
Тогда алгоритм пересчета по методу простой итерации примет вид
, 
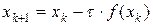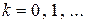. (2.6.23)
Например, возможен следующий выбор параметра .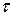
Пусть на отрезке 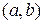существует только один корень, т.е.
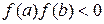и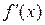 
не меняет знак на .
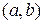Далее, пусть величина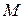 
такая, что
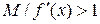для всех 
.
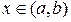Тогда в качестве параметра 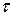можно взять значение
.
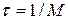В этом случае имеем:
; 
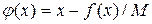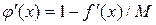, (2.6.24)
Откуда
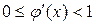. (2.6.25)
Для обеспечения на практике хорошей сходимости величина 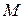не должна сильно превышать по модулю значения 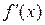. В этом случае неравенство 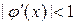будет существенно бόльшим.
Метод Ньютона. Этот метод представляется частным случаем общего метода итераций, если принять
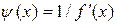. (2.6.26)
Следовательно,
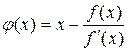(2.6.27)
и алгоритм пересчета по методу Ньютона имеет вид
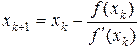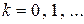, . (2.6.28)
Метод Ньютона имеет наглядую геометрическую интерпретацию. Формула касательной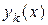 
к кривой 
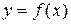в точке 
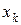имеет вид
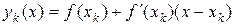(2.6.29)
Вместо корня уравнения (2.6.1)
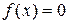
определим корень уравнения
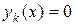, (2.6.30)
или в развернутом виде
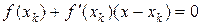
Из последнего выражения следует, что искомый корень, обозначим его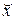 
, имеет вид
,
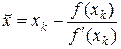т.е.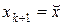 
или
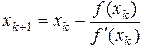
Следовательно, на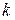 
-ом шаге итерации по методу Ньютона приближением корня функции 
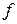является корень касательной к этой функции в точке 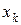, 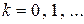. Поэтому метод Ньютона известен также как метод касательных. Рис. 2.6.3 иллюстрирует геометрическую интерпретацию итераций по методу Ньютона при заданном начальном приближении корня .
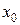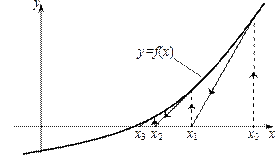
Рис. 2.6.3. Геометрическая интерпретация метода Ньютона.
Рассмотрим выполнение достаточного условия сходимости итерационного процесса по методу Ньютона. В данном случае
,
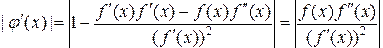откуда можно заключить, что достаточное условие сходимости имеет вид
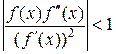или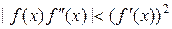 
. (2.6.31)
Замечание. Заметим, что при достаточной близости начального приближения 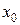к корню уравнения метод Ньютона всегда сходится.
