Операции над множествами. Над множествами можно производить действия, которые во многом напоминают действия сложения и умножения в элементар­ной алгебре

Над множествами можно производить действия, которые во многом напоминают действия сложения и умножения в элементар­ной алгебре. Для графической иллюстрации операций над множест­вами будем использовать так называемые диаграммы Эйлера, в ко­торых произвольному множеству X ставится в соответствие множе­ство точек на плоскости внутри некоторой замкнутой кривой.

Объединением (суммой) множеств X и Y называют множест­во, состоящее из всех тех элементов, которые принад­лежат хотя бы одному из множеств X, Y (рис. 1.1).

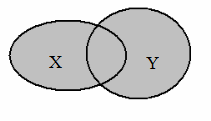Рис. 1.1. Объединение множеств

Объединение двух множеств символически записывают как X È Y. Объединение множеств X_i (i = 1, 2,..., n) есть множество элементов, каждый из которых принадлежит хотя бы одному из множеств X_i. Соответствующее обозначение:

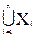
Пересечением множеств X и Y называют множество, состоя­щее из всех тех элементов, которые принадлежат как множеству X, так и множеству Y (рис. 1.2).

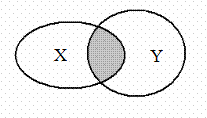Рис. 1.2. Пересечение множеств

Пересечение множеств обо­значается через X ÇY. Множест­ва X и Y называют непересе­кающимися, если они не имеют общих элементов, т.е. если X Ç Y = Æ.

Пересечением множеств Х_i (i = 1, 2,..., n) называется множест­во элементов, принадлежащих каждому X_i. Оно обозначается как

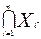
Разностью множеств X и Y называют множество, состоящее из всех тех элементов, которые принадлежат X и не принадлежат Y (рис. 1.3). Разность множеств обозначается через X \ Y. Очевидно, что X \ Y ¹ Y \ X.

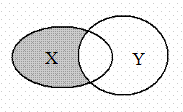
Рис. 1.3. Разность множеств

Симметрической разностью X ⊕ Y множеств X и Y называется объединение разностей X \ Y и Y \ X. Эта разность множеств является составной операцией:

X ⊕ Y = (X \ Y) È (Y \ X).

Пример 1. Пусть: X – множество отличников в группе, Y – мно­жес­тво студентов, живущих в общежитии. Тогда: X È Y – множество студентов, которые или учатся на «отлично», или прожи­вают в общежитии; X Ç Y – множество отличников, живущих в общежитии; X \ Y – множество отличников, живущих вне общежи­тия.

Дополнительным к множеству X по отноше­нию к мно­жеству W, если X Ì W, называется множе­ство, состо­я­щее из элемен­тов W, не принадлежащих мно­жеству X. Дополнительное мно­жество обозначается:Z_w(X) (рис. 1.4).

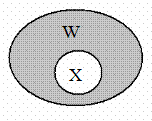
Рис. 1.4. Дополнительное множество

Универсальным множеством называется множествоI, для ко­торого справедливо соотношение: X Ç I = X. Оно означает, что мно­жество I содержит все элементы множества X. Следовательно, любое мно­жество X полностью содержится во множестве I, т.е. является его подмножеством: Х Ì I.Так, для примера 1 универсальным множеством можно считать множество студентов в группе.

Универсальное множество удобно изображать графически в виде множества точек прямоугольника. Отдельные области внутри этого прямоугольника будут представлять подмножества универсального множества.

Дополнением множества X (до уни­версального множества I) назы­вают множество `Х, определяемое из соотношения: `Х = I \ X.

На рис 1.5 множество`Х представляет со­бой не заштрихованную область.

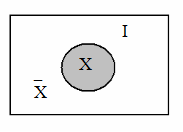
Рис. 1.5. Множество Х и его дополнение`Х

Очевидно выполнение соотношений:

X Ç`Х = Æ, X È`Х = I.

Из этого следует, что само множество X, в свою очередь, является дополнением множества `Х (до I ). Следовательно: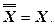

С помощью операции дополнения можно пред­ставить разность множеств в виде составной операции:

X \ Y = X Ç `Y.