Системы множеств

Элементы множества сами могут быть множествами.

Пример 1. Множество X = {1},{2,3},{1,2} состоит из

множеств:

Х₁ = {1}; Х₂ = {2,3}; Х₃ = {1,2}.

В этом случае будем говорить о системе множеств. Рассмотрим такие системы: булеан и разбиение множеств.

Булеаном В(Х) множества X называется множество всех его подмножеств. В булеан В(Х)обязательно включается само множество X и пустое множество Æ.

Пример 2. Для множества X = {0,1} булеаном является множе­ство:

В(Х) = Æ, {0},{1},{0,1}.

Разбиением P(X) множества Х называется система его непустых непере­секающихся подмножеств, в объединении дающая множество X (рис. 1.6).

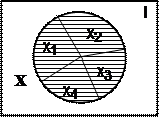
Рис. 1.6. Разбиение множества P(X) = {Х₁, Х₂, Х₃, Х₄}

Разбиение P(X) = {Х₁, Х₂,..., Х_n} множества X удовлетворяет следующим условиям:

1) X_i Ì X, i = l,..., n;

2) X_i ¹ Æ, i = l,..., n;

3) X_i Ç X_j = Æ, при i ¹ j;

4)

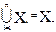
Множества Х₁, Х₂,..., Х_n называются блоками разбиения P(X). Для исходного множества Х можно получить несколько различных разбиений.

Пример 3. Для множества X = {1,2,3,4,5} можно построить следующие разбиения:

P₁(X) = {{1,2}, {3,4,5}} – из двух блоков;

P₂(Х) = {{1},{2,5},{3},{4}} – из четырех блоков.

Примерами разбиений также являются разбиения множества студентов университета по факультетам, по курсам и по группам.