Отношения эквивалентности

Бинарные отношения делятся на типы в зависимости от свойств, которыми они обладают.

Отношение R на множестве X называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметрич­ности и транзитивности.

Важной особенностью отношений эквивалентности является то, то они разбивают все множество Х на не­пересе­кающиеся подмножества – классы эквива­лент­ности.

Классом эквивалентности, порожденным элементом х Î X, называется подмножество [х] множества X, для элементов которого выполняется условие (х, у) Î R, yÎ X.

Таким образом, класс эквивалентно­сти:

[х] = {у | y Î X; (x, y) Î R}.

Классы эквивалентности образуют систему непустых непересекающихся подмножеств множества X, в объединении дающую все множество X – т. е. образуют разбиение множества Р(Х).

Обозначим отношение эквивалентности символом º, тогда класс эквивалентности записывается в виде:

[х] = {у | y Î X; х º у}.

Из рассмотренных в примере отношений только отно­ше­ние М является отношением эквивалент­ности.

Отношение М разбивает множество X = {1,2,3,4,5,6,7} на три клас­са эквивалентности:

[1] = {1,4,7}, [2] = {2,5}, [3] = {3,6}.
Классы, порожденные элементами 4, 5, 6 и 7 совпадают с этими классами:

[4] = [1], [5] = [2], [6] = [3], [7] = [1].
1.6. Отображения множеств

Пусть X и Y – два непустых множества. Закон G, согласно ко­торому любому элементу х Î X ставится в соответствие элемент у Î Y, называется однозначным отображением X в Y. Отображение является обобщением понятия функци­и, определенной на X и принимающей значения на Y.

Используются следующие эквивалентные записи:

G: X ® Y

или

у = G(x); где х Î X, у Î Y.

В случае однозначного отображения элемент у называ­ется образом элемента х, а х – прообразом у.

Возможна ситуация, когда каждому х Î X отображение G ста­вит в соответствие некоторое подмножество
G(x) Ì Y. Тогда обра­зом элемента х будет подмножество G(x). Отображение G в этом случае будет являться многозначным отображением.

Отображение является, таким образом, всюду определенным отношением и определяется тройкой множеств (X, Y, G).

Интересным является случай, когда множества X и Y совпада­ют: X = Y. Отображение G: X ® X представляет собой отображе­ние множества X самого в себя и определяется парой множеств (X, G), где G Ì X ´ X. Подробным изучением таких отображений занимается теория графов. Рассмотрим здесь лишь нескольких операций над ними.

Пусть G и Н – отображения множества X в X. Композицией этих отображений назовем отображение GH, которое определяется следующим образом:

GH(x) = G(H(x)).

В частном случае при Н = G получим отображения:

G²(x) = G(G(x)), G³(x) = G(G²(x)) и т. д.

Для произвольного S ³ 2 имеем: G^S(x) = G(G^{S -1}(x)).

Введем для общности соотношение: G⁰(x) = х. То­гда можно записать:

G⁰(x) = G(G^-1(x)) = GG^-1(x) = х.

Это означает, что G^-1(x) представляет собой обратное отобра­жение. Тогда G^-2(x) = G^-1(G^-1(x)) и т. д.

Пример. Пусть X – множество людей. Для каждого человека х Î X обозначим через G(x) множество его детей. Тогда:

G²(x) – множество внуков х,

G³(x) – множество правнуков х,

G^-1(х) – множе­ство родителей х и т. д.

Изображая людей точками и рисуя стрелки, идущие из х в G(x), получим родословное, или генеалогическое де­рево, представленное на рис. 1.10.

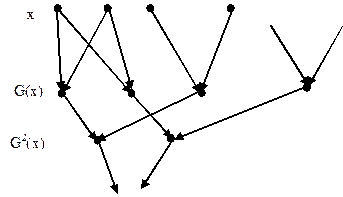
Рис. 1.10. Генеалогическое дерево