Рисунок 8.2
Рисунок 8.1
Определим мгновенную мощность, которая тратится в ребре. При этом учтем, что 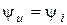 .
.
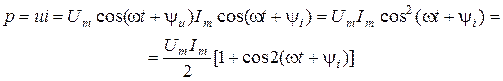 .
.
Поскольку 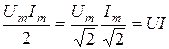 , получаем
, получаем 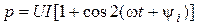 .
.
Зависимость мгновенных значений u, i, p от t (или 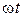 ) показана на рис.8.2. Определим активную мощность P, которая равняется среднему за период значению мгновенной мощности:
) показана на рис.8.2. Определим активную мощность P, которая равняется среднему за период значению мгновенной мощности:
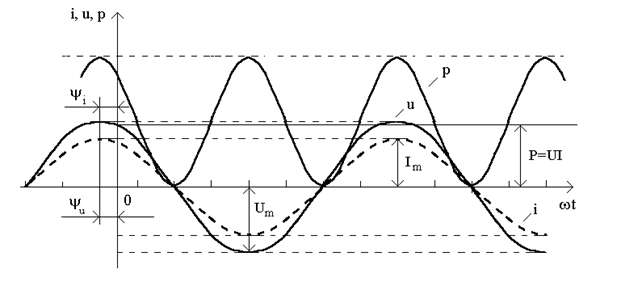
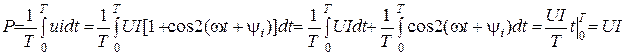 .
.
Второй интеграл равняется нулю, поскольку на интервале времени, которое кратно периоду, положительные и отрицательные площади синусоидной функции одинаковые.
8.2 Синусоидный ток в индуктивности
Пусть через индуктивность протекает ток 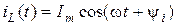 . ЭДС самоиндукции определяется по формуле
. ЭДС самоиндукции определяется по формуле 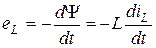 .
.
Поскольку 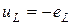 , будем иметь
, будем иметь
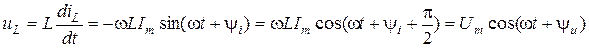 .
.
Это выражение разрешает сделать такие выводы:
1) 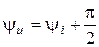 ;
; 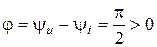 , ведь напряжение опережает ток в индуктивности на угол
, ведь напряжение опережает ток в индуктивности на угол 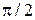 ;
;
2) амплитуды, равно как и реальные значения напряжения и тока, связаны законом Ома: 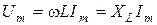 ;
; 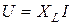 . Величина
. Величина 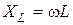 , которая измеряется в Омах, носит название индуктивного сопротивлением; обратная к ней величина
, которая измеряется в Омах, носит название индуктивного сопротивлением; обратная к ней величина 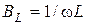 носит название индуктивной проводимости. Тогда
носит название индуктивной проводимости. Тогда  ;
; 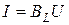 .
.
Мгновенная мощность энергии, которая поступает в индуктивность, представляет:
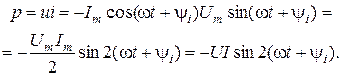
Очевидно, что активная мощность P = 0 (как среднее значение синусоидной функции на интервале времени T). Определим энергию магнитного поля в индуктивности:
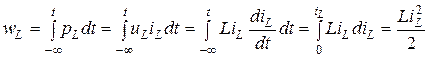 .
.
(Замена переменных в пределах: при 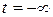 ,
, 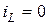 ; при
; при 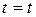 ,
, 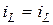 ).
).
Зависимость мгновенных значений u, i, p, 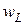 в индуктивности по времени изображена на рис.8.3. Проанализируем эти временные диаграммы: на протяжении первой четверти периода (отсчет от точки t*), когда ток в цепи увеличивается, имеет место заряд индуктивности, т.е. накопление энергии в магнитном поле за счет источника. Мгновенная мощность при этом положительная и достигает максимального значения
в индуктивности по времени изображена на рис.8.3. Проанализируем эти временные диаграммы: на протяжении первой четверти периода (отсчет от точки t*), когда ток в цепи увеличивается, имеет место заряд индуктивности, т.е. накопление энергии в магнитном поле за счет источника. Мгновенная мощность при этом положительная и достигает максимального значения 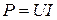 .
.
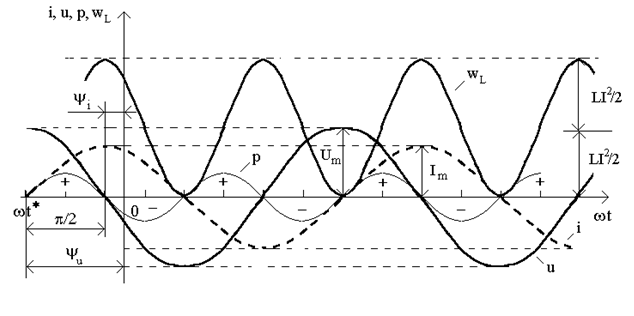 Рисунок 8.3
Рисунок 8.3
В момент времени 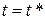 (
(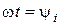 ) энергия, накопленная в магнитном поле, также достигает максимального значения
) энергия, накопленная в магнитном поле, также достигает максимального значения 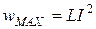 . После этого в течение следующей четверти периода происходит уменьшение тока и мгновенной энергии, т.е. разряд индуктивности; мгновенная мощность в эти моменты отрицательная. Поскольку энергия в системе не тратится (P = 0), то уменьшение
. После этого в течение следующей четверти периода происходит уменьшение тока и мгновенной энергии, т.е. разряд индуктивности; мгновенная мощность в эти моменты отрицательная. Поскольку энергия в системе не тратится (P = 0), то уменьшение 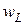 означает, что энергия возвращается к источнику. Далее процесс повторяется. Итак, происходит колебание энергии между источником и индуктивностью, причем активная мощность, которая поступает в индуктивность, равняется нулю.
означает, что энергия возвращается к источнику. Далее процесс повторяется. Итак, происходит колебание энергии между источником и индуктивностью, причем активная мощность, которая поступает в индуктивность, равняется нулю.
Подадим мгновенные значение тока и напряжения через комплексно-временные функции: 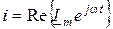 ;
; 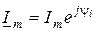 .
.
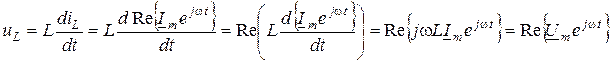 .
.
Из последнего выражения можно сделать такие выводы:
1) операция дифференцирования реальной функции времени за t эквивалентна умножению на величину 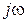 комплексно-временной функции;
комплексно-временной функции;
2) равность реальных частей между собой для любого t, возможна при условиях равности векторов: 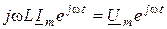 . Тогда из последнего уравнения получаем закон Ома в комплексной форме:
. Тогда из последнего уравнения получаем закон Ома в комплексной форме:
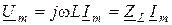 , (8.2)
, (8.2)
где 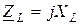 - комплексное сопротивление индуктивности.
- комплексное сопротивление индуктивности.
Рассмотрим фазовые соотношения комплексных амплитуд тока и напряжения в индуктивности. Для этого запишем 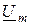 в показательной форме:
в показательной форме:
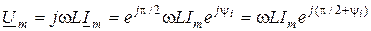 .
.
Это выражение подтверждает вывод относительно фазового сдвига между комплексными амплитудами 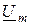 и
и 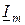 на угол
на угол 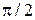 (рис.8.4а). Напомним, что положительные фазовые углы отсчитывают от оси +1 против хода часовой стрелки. Фазовый сдвиг между напряжением и током отсчитываем от вектора
(рис.8.4а). Напомним, что положительные фазовые углы отсчитывают от оси +1 против хода часовой стрелки. Фазовый сдвиг между напряжением и током отсчитываем от вектора 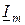 до вектора
до вектора 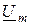 .
.
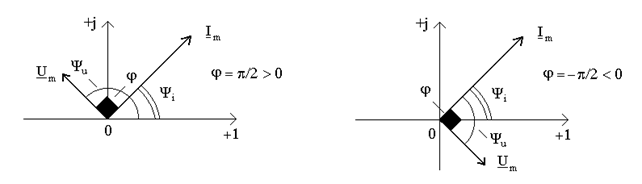
а) б)
 2014-02-09
2014-02-09 590
590








