Рисунок 7.5
Рисунок 7.4
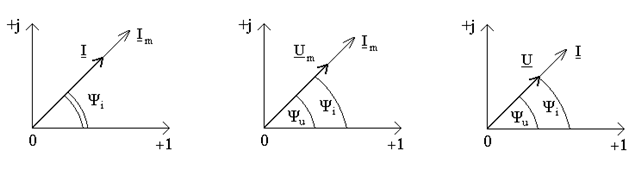
Рисунок 7.3
Рисунок 7.2
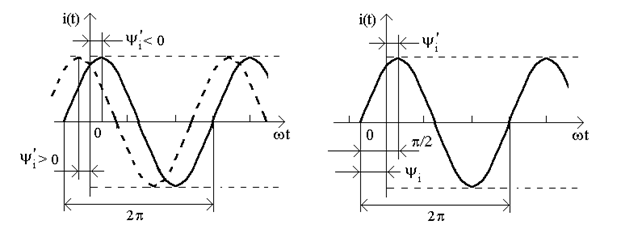
Начальная фаза синусоидного электрического тока – значение фазы синусоидного тока в начальный момент времени (t =0). Иначе, начальная фаза соответствует абсцисссе ближайшей точки перехода с отрицательной полуволны к положительной. На рис.7.2а начальная фаза колебания равняется нулю, на рис.7.2б первая кривая имеет начальную фазу 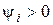 , которой отвечает
, которой отвечает 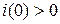 , а вторая кривая -
, а вторая кривая - 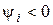 , так как
, так как 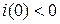 .
.
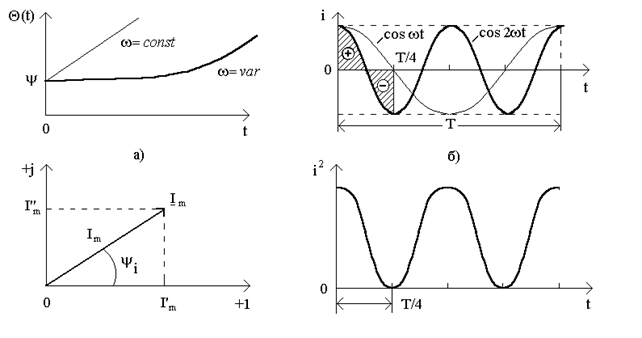
Если рассматривать сменный ток, который описывается косинусоидным законом 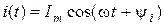 , то как начальная фаза используется абсциссса ближайшего положительного максимума (рис.7.3а). Рис.7.3б показывает соотношение начальных фаз при синусоидном и косинусоидном формах записи:
, то как начальная фаза используется абсциссса ближайшего положительного максимума (рис.7.3а). Рис.7.3б показывает соотношение начальных фаз при синусоидном и косинусоидном формах записи:
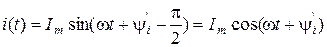 .
.
Итак, при переходе от синусоидной к косинусоидной форме записи начальная фаза уменьшается на 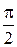 , при обратном переходе - на
, при обратном переходе - на 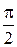 увеличивается.
увеличивается.
а) б)
Пусть для некоторого участка электрического цепи ток и напряжение представляют: 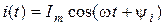 ;
; 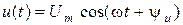 , тогда величина
, тогда величина 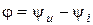 носит название сдвигом фаз между напряжением и током. Это понятие устанавливается для характеристики двух колебаний одинаковой частоты.
носит название сдвигом фаз между напряжением и током. Это понятие устанавливается для характеристики двух колебаний одинаковой частоты.
Итак, сдвиг фаз между напряжением и током - это алгебраическая величина, которая равняется разнице начальных фаз напряжения и тока.
Если 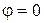 , колебания (т.е. ток и напряжение) синфазны;
, колебания (т.е. ток и напряжение) синфазны;
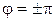 , колебание противофазные;
, колебание противофазные;
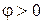 ,
, 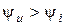 - напряжение опережает ток на величину
- напряжение опережает ток на величину 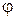 ;
;
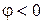 ,
, 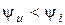 - напряжение отстает от тока на величину
- напряжение отстает от тока на величину 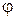 .
.
Эти соотношения справедливы также и для синусоидной формы записи. Аргумент синуса (косинуса) представляет собой мгновенную или текущую фазу 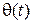 :
: 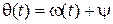 . Связь между угловой частотой
. Связь между угловой частотой 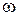 и текущей фазой
и текущей фазой 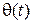 устанавливается соотношениями:
устанавливается соотношениями:
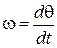 ;
; 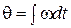 .
.
На рис.7.4а показана зависимость 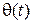 при
при 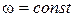 и
и 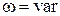 .
.
в) г)
Чтобы определить действующее значение синусоидного тока, воспользуемся формулой (7.1) и косинусоидной формой записи 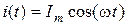 (
(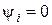 ).
).
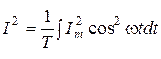 .
.
Заменим 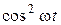 на
на 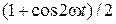 и проинтегрируем полученное выражение:
и проинтегрируем полученное выражение:
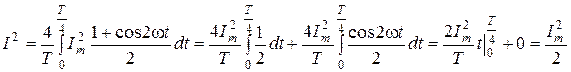 .
.
Второй интеграл равняется нулю, поскольку функция 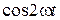 на интервале 0¸ T /4 имеет одинаковые положительную и отрицательную площади (рис.7.4б).
на интервале 0¸ T /4 имеет одинаковые положительную и отрицательную площади (рис.7.4б).
Итак, действующее значение связано с амплитудным: 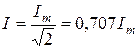 , т.е. амплитудное значение всегда больше, чем действующее.
, т.е. амплитудное значение всегда больше, чем действующее.
Действующее значение синусоидного тока характеризует его энергетическое действие. Вольтметры и амперметры в цепях сменного тока показывают действующее значение ЭДС, напряжения и тока. Например, если амплитуда напряжения в цепи U = 311 В, то вольтметр на зажимах цепи покажет 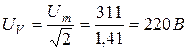 .
.
7.3 Представление синусоидних колебаний в виде проекций вращающихся векторов
Для расчета электрических цепей синусоидного тока применяют метод комплексных амплитуд (или символичный метод), который разрешает рассчитывать эти цепи алгебраическим способом, аналогично цепям постоянного тока. Комплексный метод основан на изменении синусоидных функций времени вращающимися векторами.
Известно, что каждая точка на комплексной плоскости определяется вектором, начало которого находится в нуле, а конец - в точке, что соответствует данному комплексному числу. Комплексное число можно выразить в трех формах: в показательной (
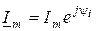 -
-
где 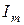 - модуль комплексного числа;
- модуль комплексного числа; 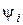 - аргумент (рис.7.4г);
- аргумент (рис.7.4г);
в тригонометричной - 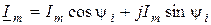 ;
;
в алгебраической (
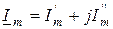 ,
,
где 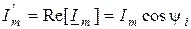 - реальная часть;
- реальная часть;
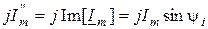 - мнимая часть комплексного числа.
- мнимая часть комплексного числа.
Очевидно, что
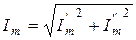 ;
; 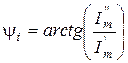 .
.
Вращаемый вектор в положительном направлении (т.е. против часовой стрелки) с угловой скоростью 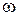 , можно подать как комплексно-временную функцию
, можно подать как комплексно-временную функцию
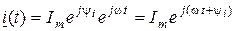 , (7.2)
, (7.2)
где 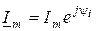 - комплексная амплитуда;
- комплексная амплитуда; 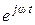 - оператор поворота (вращения).
- оператор поворота (вращения).
Итак, комплексная амплитуда синусоидного тока (напряжения) - это комплексная величина, модуль и аргумент которой равняются соответственно амплитуде и начальной фазе синусоидного тока (напряжения).
Комплексная амплитуда не зависит от времени, т.е. является недвижимым вектором. Умножение комплексной амплитуды 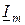 на
на 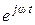 означает поворот вектора
означает поворот вектора 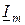 на комплексной плоскости в положительном направлении на угол
на комплексной плоскости в положительном направлении на угол 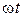 .
.
Записывая комплексно-временную функцию (7.2) в тригонометрической форме
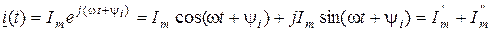 ,
,
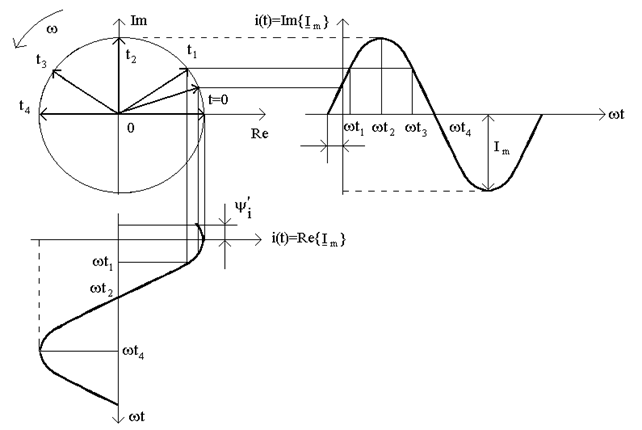
видим, что синусоидная функция i (t) может рассматриваться как мнимая часть (7.2) или как проекция вектора 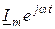 на мысленную ось:
на мысленную ось:
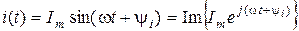 .
.
Обозначение Im означает, что применяется мнимая часть ("image").
Аналогично косинусоидная функция может рассматриваться как реальная часть или проекция на реальную ось:
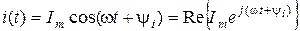 .
.
Символ Re означает операцию взятия реальной части ("real").
Представление синусоидной функции с помощью векторов и их проекций показывается на рис.7.5.
8.1 Синусоидный ток в ребре
Рассмотрим цепь с резистором, которая имеет активное сопротивление R. Пусть в цепи протекает ток 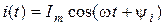 . Тогда по закону Ома напряжение на зажимах резистора будет представлять:
. Тогда по закону Ома напряжение на зажимах резистора будет представлять:
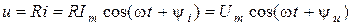 .
.
Как видим, 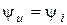 ;
; 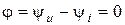 , т.е. напряжение и ток в цепи с активным сопротивлением сходятся по фазе. Кроме того, при прохождении синусоидного тока сквозь сопротивление не только мгновенные значения, но и амплитуды и действительные значения связаны по закону Ома:
, т.е. напряжение и ток в цепи с активным сопротивлением сходятся по фазе. Кроме того, при прохождении синусоидного тока сквозь сопротивление не только мгновенные значения, но и амплитуды и действительные значения связаны по закону Ома:
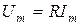 ;
; 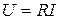 .
.
Подадим мгновенные значение напряжения и тока через комплексно-временные функции:
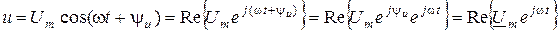 ;
;
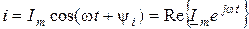 .
.
Подставим эти значения к выражению 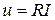 :
:
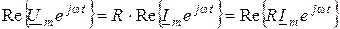 .
.
Если равны в любое время между собой реальные части, то равны и векторы: 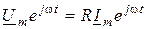 . Сократив на множитель
. Сократив на множитель 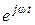 , будем иметь
, будем иметь
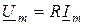 . (8.1)
. (8.1)
Это уравнение является законом Ома в комплексной форме.
Запишем комплексные реальные значения тока и напряжения:
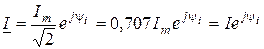 ;
; 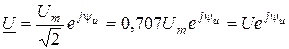 .
.
На рис.8.1 изображены векторы 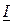 ,
, 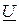 ,
, 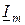 ,
, 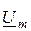 на комплексной плоскости.
на комплексной плоскости.
 2014-02-09
2014-02-09 795
795








