Рисунок 9.4
Рисунок 9.3
Рисунок 9.2
Рисунок 9.1
Вывод. Геометрическая сумма векторов 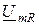 ,
, 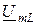 ,
, 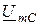 дает вектор приложенного к цепи напряжения:
дает вектор приложенного к цепи напряжения: 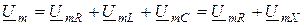 . Прямоугольный треугольник, катетами которого есть
. Прямоугольный треугольник, катетами которого есть 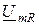 i
i 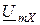 , а гипотенуза равняется
, а гипотенуза равняется 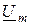 , носит название треугольником напряжений.
, носит название треугольником напряжений.
Если все стороны-векторы этого треугольника поделить на вектор 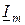 , получим треугольник ребер, подобный треугольнику напряжений и повернутый относительно последнего на угол
, получим треугольник ребер, подобный треугольнику напряжений и повернутый относительно последнего на угол 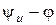 по ходу часовой стрелки (рис.9.2). Треугольник ребер есть геометрической интерпретацией уравнения (9.5). Его положение не зависит от начальных фаз
по ходу часовой стрелки (рис.9.2). Треугольник ребер есть геометрической интерпретацией уравнения (9.5). Его положение не зависит от начальных фаз 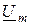 и
и 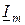 ; активное сопротивление R откладывается на комплексной плоскости в положительном направлении реальной оси, а реактивное сопротивление X в зависимости от его знака откладывается по положительной (X > 0), или отрицательной мысленной оси (рис.9.2а,б).
; активное сопротивление R откладывается на комплексной плоскости в положительном направлении реальной оси, а реактивное сопротивление X в зависимости от его знака откладывается по положительной (X > 0), или отрицательной мысленной оси (рис.9.2а,б).
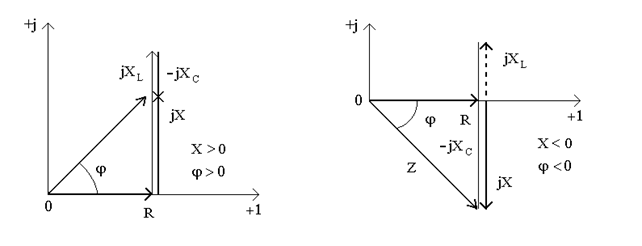
а) б)
В треугольнике ребер угол 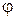 отсчитывается от положительной действительной осик вектору Z (как аргумент этого вектора) и совпадает с соответствующим значением сдвига фаз между напряжением и током (рис.9.1), который следует отсчитывать от вектора тока
отсчитывается от положительной действительной осик вектору Z (как аргумент этого вектора) и совпадает с соответствующим значением сдвига фаз между напряжением и током (рис.9.1), который следует отсчитывать от вектора тока 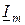 к вектору напряжения
к вектору напряжения 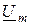 .
.
9.2 Параллельное соединение элементов R, L, C
Рассуждая аналогично, найдем комплексную форму законов Ома и Кирхгофа для электрической цепи, которая состоит из параллельно соединенных элементов R, L, C. Запишем уравнения по первому закону Кирхгофа для мгновенных значений токов:
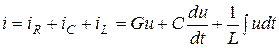 . (9.6)
. (9.6)
Перейдем от мгновенных значений i, u к комплексно-временным функциям:
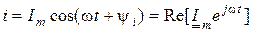 ;
; 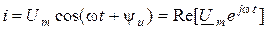 .
.
Подставив эти значения к (9.6), получим уравнения для комплексных амплитуд:
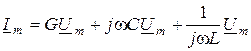 . (9.7)
. (9.7)
Учитывая, что 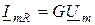 ;
; 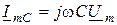 ;
; 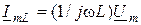 , находим выражение для первого закона Кирхгофа в комплексной форме:
, находим выражение для первого закона Кирхгофа в комплексной форме:
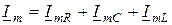 . (9.8)
. (9.8)
Если вынести в (9.7) значение 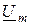 за скобки, получим
за скобки, получим
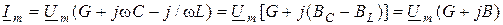 ,
,
где 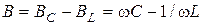 - реактивная проводимость цепи; G - активная проводимость цепи;
- реактивная проводимость цепи; G - активная проводимость цепи; 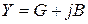 - комплексная проводимость цепи.
- комплексная проводимость цепи.
Так же, как и формула (9.4), уравнения
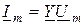 ,
, 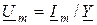 (9.9)
(9.9)
подают закон Ома в комплексной форме.
Итак, комплексная проводимость цепи - комплексная величина, которая равняется частице от деления комплексного тока на комплексное напряжение на зажимах пассивной электрической цепи. Комплексная проводимость может быть представленна в тригонометричной и показательной формах:
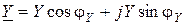 ;
; 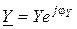 , (9.10)
, (9.10)
где 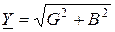 - модуль комплексной проводимости
- модуль комплексной проводимости 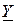 или полная электрическая проводимость;
или полная электрическая проводимость; 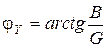 - аргумент комплексной проводимости
- аргумент комплексной проводимости 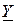 ;
; 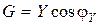 - активная проводимость (реальная часть комплексной проводимости);
- активная проводимость (реальная часть комплексной проводимости); 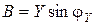 - реактивная проводимость (мнимая часть комплексной проводимости).
- реактивная проводимость (мнимая часть комплексной проводимости).
На основе (9.9) запишем: 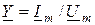 . Тогда
. Тогда
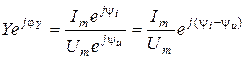 .
.
Итак, полная проводимость 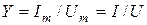 - это скалярная величина, которая равняется частице от деления действующего (амплитудного) значения тока в двуполюснике на действующее (амплитудное) значение напряжения на его зажимах. Аргумент комплексной проводимости
- это скалярная величина, которая равняется частице от деления действующего (амплитудного) значения тока в двуполюснике на действующее (амплитудное) значение напряжения на его зажимах. Аргумент комплексной проводимости 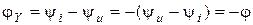 с точностью к знаку обуславливает фазовый сдвиг в цепи.
с точностью к знаку обуславливает фазовый сдвиг в цепи.
Изобразим векторные диаграммы. На рис.9.3 представлена геометрическая интерпретация на комплексной плоскости уравнения (9.8). Рис.9.3а соответствует варианту, когда реактивная проводимость цепи имеет индуктивный характер (B < 0), ток отстает по фазе от напряжения, а напряжение опережает ток по фазе на угол 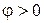 . Рис.9.3б соответствует случаю, когда реактивная проводимость цепи имеет емкостной характер (B > 0), напряжение отстает по фазе от тока на угол
. Рис.9.3б соответствует случаю, когда реактивная проводимость цепи имеет емкостной характер (B > 0), напряжение отстает по фазе от тока на угол 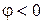 (ток опережает напряжение).
(ток опережает напряжение).
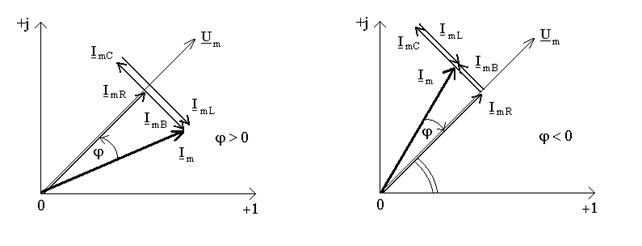
а) б)
Прямоугольный треугольник с катетами 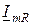 и
и 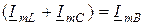 и гипотенузой
и гипотенузой 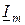 носит название треугольника токов;
носит название треугольника токов; 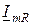 и
и 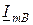 есть соответственно активной и реактивной составляющими тока
есть соответственно активной и реактивной составляющими тока 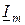 .
.
Если все стороны этого треугольника поделить на вектор 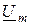 , то получим треугольник проводимостей, подобный треугольнику токов и повернутый относительно последнего на угол
, то получим треугольник проводимостей, подобный треугольнику токов и повернутый относительно последнего на угол 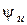 по ходу часовой стрелки. Треугольник проводимостей есть геометрической интерпретацией выражения (9.10). Активная проводимость G откладывается на комплексной плоскости в положительном направлении реальной оси, а реактивная проводимость B в зависимость от ее знака откладывается в отрицательном (B < 0) или в положительном (B > 0) направлении мнимой оси (рис.9.4а,б).
по ходу часовой стрелки. Треугольник проводимостей есть геометрической интерпретацией выражения (9.10). Активная проводимость G откладывается на комплексной плоскости в положительном направлении реальной оси, а реактивная проводимость B в зависимость от ее знака откладывается в отрицательном (B < 0) или в положительном (B > 0) направлении мнимой оси (рис.9.4а,б).
В треугольнике проводимостей угол 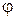 отсчитывается от гипотенузы Y к катету G аналогично к треугольнику токов, где угол
отсчитывается от гипотенузы Y к катету G аналогично к треугольнику токов, где угол 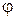 отсчитывается от
отсчитывается от 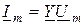 к
к 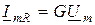 .
.

а) б)
 2014-02-09
2014-02-09 888
888








