Возможные значения с. в. Х: 0; 1; 2; 3; 4; 5 –попаданий при пяти выстрелах. Условия задачи соответствуют требованиям, при которых справедлива формула Бернулли. Если вероятность попадания при каждом выстреле равна р = 0,6, то вероятность противоположного события – промаха, равна q = 0,4. Посчитаем вероятности возможных значений:


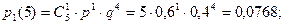
И т. д. Ряд распределения случайной величины Х будет иметь вид:
 xi xi
| ||||||
| pi | 0,01024 | 0,0768 | 0,2304 | 0,3456 | 0,2592 | 0,0777 |
Математическое ожидание:
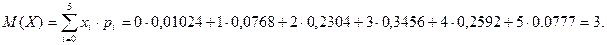
Пример. непрерывная с. в. Х задана плотностью распределения:
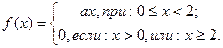 Найти математическое ожидание М(Х).
Найти математическое ожидание М(Х).
Решение.
В формуле, задающей плотность распределения, содержится неизвестный параметр а. Для его определения используем свойство 4 плотности распределения.
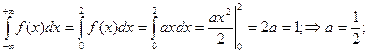
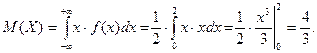
Размерность математического ожидания совпадает с размерностью случайной величины.
Второй числовой характеристикой случайной величины является характеристика, показывающая, как сильно её возможные значения разбрасываются вокруг математического ожидания (среднего значения).
Механическим аналогом характеристики рассеивания для дискретной случайной величины является момент инерции материальных точек, размещённых определённым образом на числовой оси, относително своего центра тяжести, при этом суммарная масса точек равна единице.
В теории вероятности эта характеристика получила название «дисперсия» D(X).
Пусть дискретная с. в. задана своим рядом распределения (см. табл. выше). Тогда её дисперсия (по аналогии с моментом инерции) будет иметь вид:
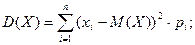
Механическим аналогом дисперсии для непрерывной случайной величины служит момент инерции тонкого прямого стержня, размещённого определённым образом на числовой оси, относительно его центра тяжести, причём масса стержня равна единице и известен закон распределения его линейной плонности.
Пусть возможные значения непрерывной случайной величины заполняют промежуток числовой оси 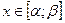 , а его плотность распределения задана функцией f(x). Тогда её дисперсия будет иметь вид:
, а его плотность распределения задана функцией f(x). Тогда её дисперсия будет иметь вид:
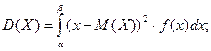
При вычислении дисперсии удобно пользоваться другими формулами, которые получим из вышеприведенных:

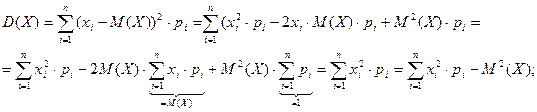
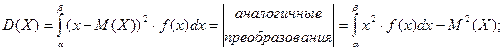
Определение. Дисперсия равна математическому ожиданию квадрата случайной величины без квадрата её математического ожидания.
Если возможных значений дискретной случайной величины - бесконечное, но счётное множество, или если непрерывная случайная величина принимает свои значения на всей числовой оси, то формулы для дисперсии принимают вид:
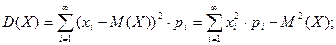
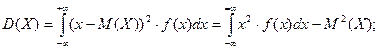
Свойства дисперсии.
1. D(C) =0, если С- константа;
2. D(CX)=C2D(X);
3. D(X+Y)=D(X)+D(Y), здесь Х и У – случайные величины;
4. D(aX+b)=a2D(X), здесь а и в - константы.
Размерность дисперсии равна квадрату размерности самой слчайной величины.
Наряду с дисперсией широкое применение находит ещё одна характеристика рассеивания, называемая средним квадратическим отклонением (с.к.о.), которое обозначается символом 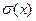 . Вычисляется с.к.о. через дисперсию по формуле:
. Вычисляется с.к.о. через дисперсию по формуле: 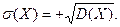 Размерность с.к.о. совподает с размерностью самой случайной величины.
Размерность с.к.о. совподает с размерностью самой случайной величины.
Свойства с.к.о.
1. 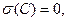 если с – константа;
если с – константа;
2. 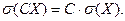
3. 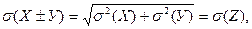 если Z = Х
если Z = Х 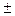 У, где Х и У – случайные величины;
У, где Х и У – случайные величины;
4. 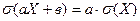 , здесь а и в – константы.
, здесь а и в – константы.
Вспомогательные числовые характеристики случайных величин.
К вспомагательным характеристикам с.в. относятся мода и медиана.
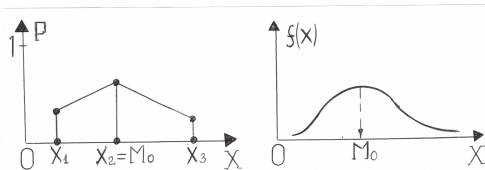
Определение. Модой М0 дискретной с. в. называется её наиболее вероятное значение.
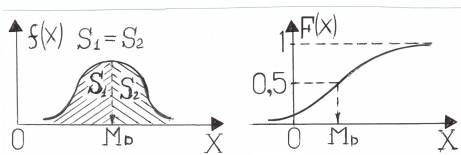
Определение. Модой М0 непрерывной с. в. называетсятакое её значение, при котором плотность распределения f(х) имеет максимум.
На приведенных ниже рисунках показаны случаи одномодального распределения, хотя возможны и двухмодальные распределения.
Определение. Медианой МD непрерывной с. в. Х называется такое её значение, относительно которого равновероятно получение большего или меньшего значения: Р(Х<MD)=P(X>MD).
Геометрически – это точка оси ОХ, ордината в которой делит площадь под кривой распределения плотности f(x) пополам, или точка оси ОХ, в которой функция распределения F(x) = 0,5.
Медианой как числовой характеристикой случайной величины обычно пользуются применительно к непрерывным случайным величинам, хотя формально её можно определить и по отношению к дискретным случайным величинам.
Арифметические операции над случайными величинами.
Пусть две дискретные случайные величины Х и У заданы своим рядом распределения.
| Х | х1 | х2 | х3 | 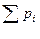
|
| р | р1 | р2 | р3 |
| У | у1 | у2 | 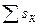
|
| s | s1 | s2 |
Закон распределения суммы Х + У двух случайных величин имеет вид:
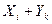
| 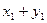
| 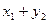
| 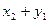
| 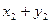
| 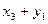
| 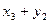
| 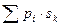
|
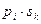
| 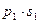
| 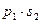
| 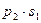
| 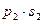
| 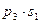
| 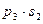
|
Закон распределения произведения ХУ двух случайных величин имеет вид:
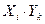
| 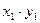
| 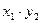
| 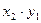
| 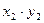
| 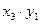
| 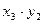
| 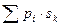
|
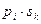
| 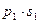
| 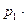 s2 s2
|  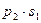
| 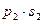 
| 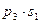
| 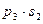
|
 2014-02-09
2014-02-09 791
791








