Примеры. 1. Случайная величина Х задана своим рядом распределения

1. Случайная величина Х задана своим рядом распределения. Построить функцию и многоугольник рсспределения, найти числовые характеристики распределения – математическое ожидание, дисперсию, среднее квадратическое отклонение и наиболее вероятное значение – моду.

Решение.

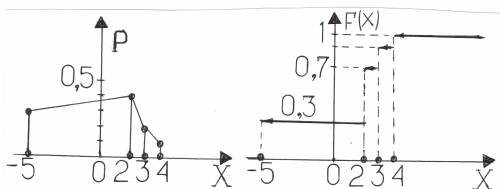
Многоугольник распределения и функция распределения F(х) приведены

на рисунках, расположенных ниже. Наиболее вероятное значение заданной случайной величины М₀ = 2.

Математическое ожидание: М(Х) = 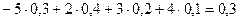ед. с.в.

Дисперсия: D(X) = 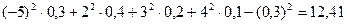ед² с.в.

Среднее квадратическое отклонение: 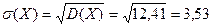ед. с.в.

Мода распределения равна: M_D =2 ед. с.в.

2. Случайная величина Х задана плотностью распределения f(x).

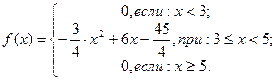
Найти функцию распределения F(x), построить графики функции распределения и плотности распределения, определить числовые характеристики случайной величины.

Решение.

Функцию распределения находим по формуле:

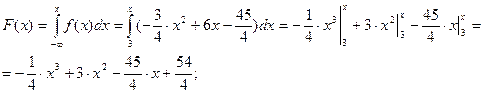
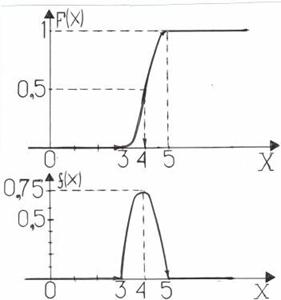
Графики функции распределения и плотности распределения приведены ниже.

Математическое ожидание: 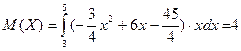ед. с. в.

Дмсперсия: 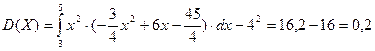ед² с. в.

С.к.о.: 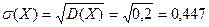ед. с. в.

Для нахождения моды найдём экстремум графика плотности:

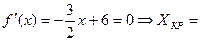M₀= 4 ед. с. в.

Медиану найдём, используя плотность распределения:

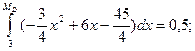
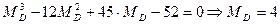ед. с. в.