Потенциальное поле

Векторное поле 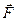называется потенциальным (или безвихревым или градиентным), если во всех точках поля ротор равен нулю,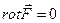

Основные свойства потенциального поля:

1) Циркуляция потенциального поля 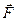по любому замкнутому контуру в этом поле равна нулю.

Для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю; в поле скоростей текущей жидкости, равенство Ц=0 означает, что в потоке нет замкнутых струй, т.е. нет водоворотов. В потенциальном поле отсутствуют вихри.

2) В потенциальном поле 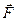криволинейный интеграл 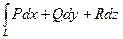вдоль любой кривой L с началом в точке 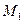и концом в точке 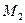зависит только от положения точек 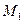и 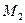и не зависит от формы кривой.

3) Потенциальное поле является полем градиента некоторой скалярной функции U(x,y,z), т.е. если 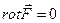, то функция U(x,y,z) такая, что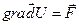

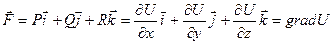
Потенциальное поле определяется заданием одной скалярной функции

U=U(x,y,z) – его потенциал.

Потенциал векторного поля может быть найден по формуле

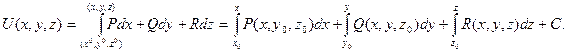
Пример: Установить потенциальность поля 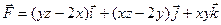и найти его потенциал.

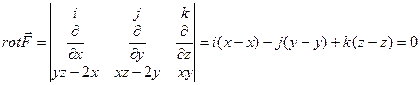
В качестве фиксированной точки (х₀, y₀, z₀) возьмем точку (0;0;0)

U(x,y,z) =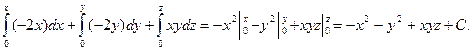

Примером потенциального поля является электрическое поле напряженности 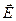точечного заряда q.