Векторные дифференциальные операции второго порядка

После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно снова применить этот оператор. В результате получаются дифференциальные операции второго порядка.

диф. операции 1-го порядка диф. операции 2-го порядка

U(M)		grad U(M)		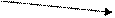div grad U(M)
	rot grad U(M)
		div	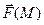	grad div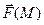
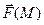				div rot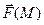
		rot	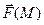	rot rot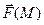

Существует пять дифференциальных операций второго порядка. Запишем некоторые формулы для дифференциальных операций 2-го порядка:

1. div grad U =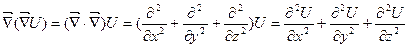

Наряду с оператором Гамильтона в векторном анализе и его приложениях используется оператор Лапласа, обозначаемый символом ∆. Оператор Лапласа определен следующей формуло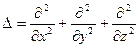й - или .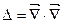

Выражение для div grad U можно записать следующим образом

div grad U=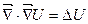

2. Применяя оператор Гамильтона легко получить 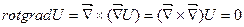, т.к. векторное произведение двух одинаковых векторов равно нулю. Это означает, что поле градиента есть безвихревое поле.

3. 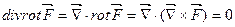, т.к. смешанное произведение трех векторов, из которых два одинаковые, равно нулю. Это означает, что поле вихря – соленоидальное, не имеет источников и стоков.