2014-02-09
1507
При расчётах электрических цепей наибольшие трудности вызывают преобразования соединения ветвей треугольником в эквивалентное соединение звездой и наоборот, так как такие соединения не могут быть заменены одним эквивалентным элементом.
Пусть между выводами 1, 2 и 3 электрической схемы включены комплексные сопротивления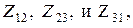 
образующие стороны треугольника (рис. 7.3 а). Токи через эти сопротивления обозначим с аналогичными индексами 
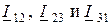, а токи 
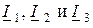в неразветвлённых участках схемы имеют индексы, совпадающие с номером соответствующего узла.
Согласно понятию эквивалентности замена соединения треугольником на эквивалентную звезду не должна менять величин токов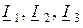 
и напряжений 
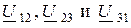между соответствующими узлами схемы (рис. 7.3 б).
В схеме соединения треугольником по первому закону Кирхгофа для узлов 1 и 2 имеем выражения
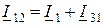(7.6 а) и 
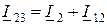(7.6 b),
в которых общим элементом является ток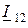 
.
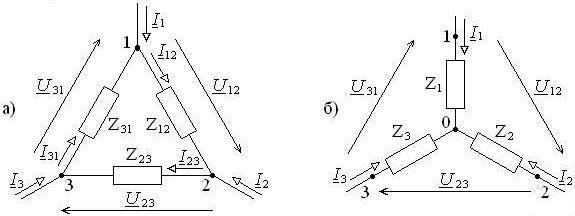
Рис. 7.3. Соединение ветвей треугольником (а) и звездой (б)
Используя формулу (7.6 а), выразим ток ветви "3-1" через ток :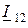
По второму закону Кирхгофа для этой же схемы имеем уравнение
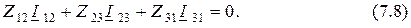
Подставляя выражения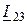 
из формулы (7.6 b) и 
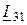из (7.7) в уравнение (7.8), получаем формулу
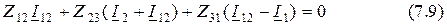
и после преобразования
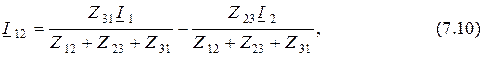
что позволяет записать формулу напряжения между выводами 1 и 2 в виде
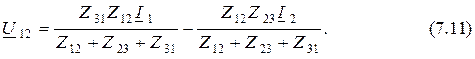
В то же время для эквивалентной схемы соединения звездой имеем выражение
Сравнивая уравнения (7.11) и (7.12), получаем условия эквивалентности схем
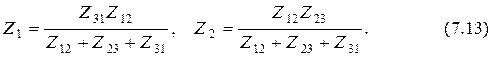
Для третьего узла по первому закону Кирхгофа имеем равенство
Преобразуя уравнение (7.6 b) к виду
и подставляя выражения (7.14) и (7.15) в уравнение (7.8), получаем зависимость
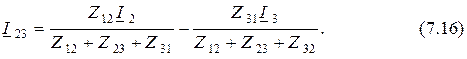
Выражая напряжение между узлами 2 и 3 через ток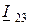 
по (7.16) для схемы соединения ветвей треугольником
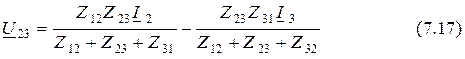
и через токи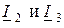 
для схемы соединения звездой
после сравнения полученных формул получаем третье условие эквивалентности схем
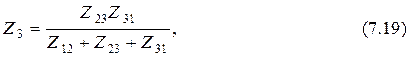
которое можно было бы получить формально путём круговой заменой индексов в выражениях (7.13).
