Частное положение плоскости в пространстве

Частное положение плоскости в пространстве

1. Проецирующее положение плоскости: перпендикулярное одной плоскости проекций;

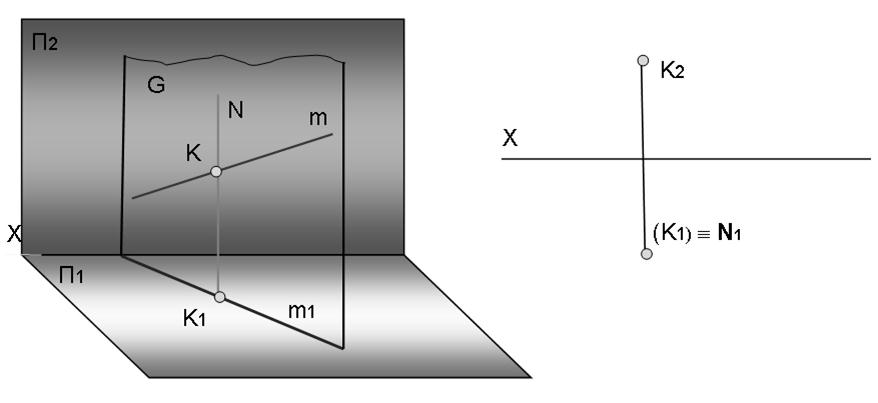
а)Горизонтально-проецирующее, ^ П₁;

Прямая N – нормаль к плоскости П₁: N принадлежит G(N ∩ m = K), m не ┴ П1;

Вывод:

Если прямая N проецируется в точку на П₁, а прямая m₁ проходит не параллельно оси Х, то вся плоскость G проецируется на П₁ в прямую линию под углом β к П₂.

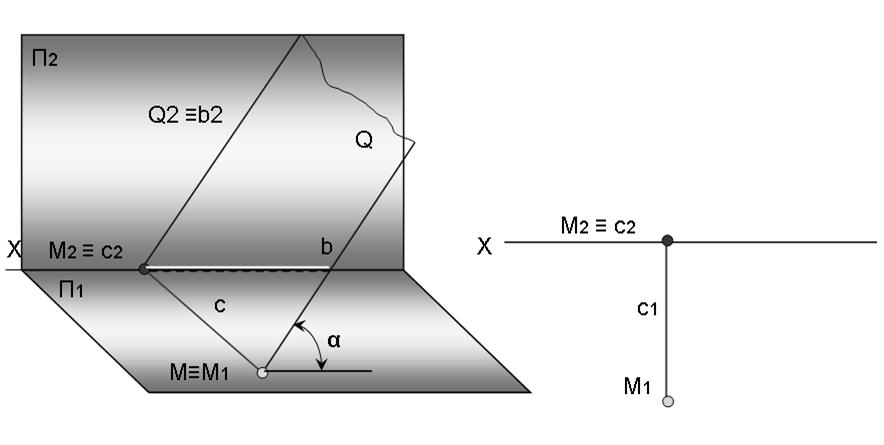
б)Фронтально-проецирующая плоскость, перпендикулярная плоскости проекций П₂

Задаем плоскость Q(с∩b = M); Прямая с ^ П₂, а прямая b образует сплоскостью П₁ угол α;

Вывод:

Фронтальная проекция плоскости Q₂ - прямая линия и наклонена к П₁ под углом α.

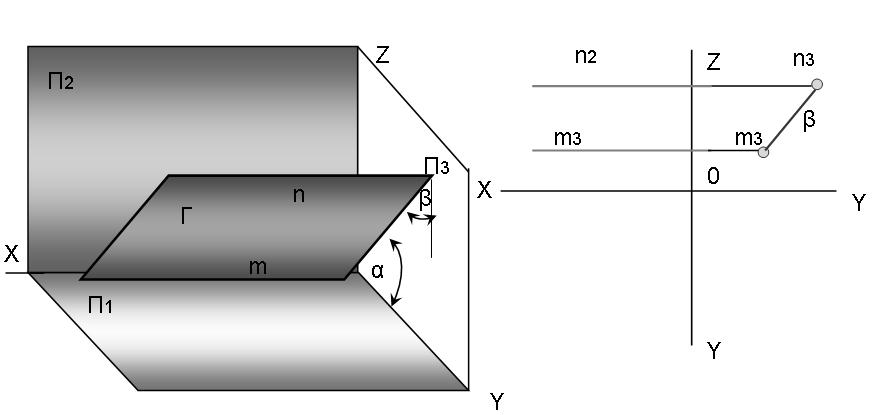
в)Профильно-проецирующая плоскость, перпендикулярна П₃.

Зададим плоскость Г(m //n), при этом m и n проходят перпендикулярно П₃.

Вывод:

Прямые m и n проецируются на П₃ в точки, а вся плоскость Г – в прямую линию;

Углы наклона плоскости Г к П₁ - α, а к плоскости П₂ – β.

Горизонтально-проецирующее -;

Фронтально-проецирующая плоскость -,

Профильно-проецирующая плоскость -,

Плоскости уровня – параллельные одной плоскости проекций

а) Плоскость горизонтального уровня: плоскость параллельная П₁

Плоскость Q(l // k) // П₁: все точки и линии, принадлежащие данной плоскости равноудалены от плоскости проекций П₁.

Вывод:

Фронтальная проекция плоскости горизонтального уровня проходит параллельно оси Х, а горизонтальная проекция служит для определения действительного вида плоской фигуры.

б)Плоскость фронтального уровня – параллельная плоскости проекций П₂

• Плоскость Г (а ∩ с = K)// П₂:

Все линии принадлежащие такой плоскости равноудалены от П₂, т.е. Y всех ее точек одинаковы.

Вывод:

Фронтальная проекция плоскости Г проходит параллельно оси Х, а горизонтальная служит для определения действительного вида плоских фигур данной плоскости.