По-прежнему принимаем, что каждое предприятие сообщает Центру оценку 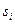 параметра
параметра 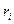 , функции затрат
, функции затрат 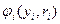 и тем самым оценку
и тем самым оценку
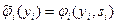
функции затрат. На основе этой информации Центр решает задачу минимизации суммарных затрат
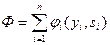 (5.1)
(5.1)
при условии
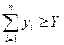 (5.2)
(5.2)
В качестве целевой функции предприятия примем разность получаемых средств 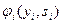 и фактически потраченных
и фактически потраченных 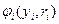 , то есть
, то есть
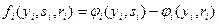 (5.3)
(5.3)
Проведем исследование механизма компенсации для функций затрат вида 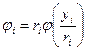 и гипотезе слабого влияния. Учитывая, что в оптимальном решении
и гипотезе слабого влияния. Учитывая, что в оптимальном решении
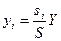 ,
, 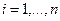 ,
,
получаем условия оптимальности
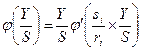
или
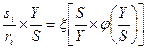 . (5.4)
. (5.4)
Из (5.4) получаем
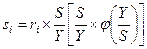 ,
, 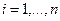 . (5.5)
. (5.5)
Суммируя (5.5) по всем предприятиям, получаем
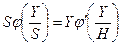 . (5.6)
. (5.6)
Левая часть этого равенства равна сумме средств, выплачиваемых предприятиям при механизме компенсации, а правая, как легко убедиться, равна сумме средств, выплачиваемых предприятиям при механизме стимулирования. Таким образом, мы получили весьма важный вывод.
Теорема 2. Механизм компенсации эквивалентен механизму стимулирования в том смысле, что в обоих случаях Центр выплачивает предприятиям одну и ту же сумму средств.
Из (.5.5) и (5.6) получаем
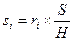 ,
, 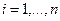 . (5.7)
. (5.7)
Пример 3. Пусть 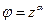 . В этом случае уравнение (5.6) принимает вид
. В этом случае уравнение (5.6) принимает вид
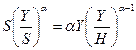 ,
,
решая которое относительно S, получаем
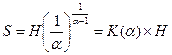 (5.8)
(5.8)
Зависимость 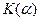 показана на рис. 1.
показана на рис. 1.
Заметим, что
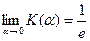
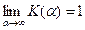 .
.
 2014-02-09
2014-02-09 466
466








