2014-02-09
417
Множество победителей определяется в результате прямого решения задачи на максимум суммарного эффекта (6.1) при ограничении 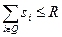(6.5)
(6.5)
Примем далее, что каждое предприятие представляет на конкурс только один проект.
Теорема 3. Эффективность прямого конкурса не менее 0,5.
Доказательство. Пусть Q - множество победителей прямого конкурса. Очевидно, что предприятия, проекты которых не вошли в число победителей, будут сообщать объективные оценки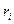 
в надежде попасть в число победителей (меньше 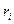сообщать не целесообразно, поскольку 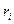определяет минимальный объем финансирования, необходимый для успешной реализации проекта). Обозначим через P множество предприятий, не вошедших в число победителей, и рассмотрим следующую задачу: определить 
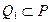, максимизирующее
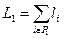
при ограничении (6.2).
Очевидно, что 
, где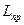 
- значение 
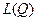в оптимальном решении задачи (6.1), (6.2). Заметим также, что
.
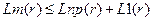Имеем
.
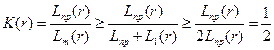Полученная оценка является точной, что показывает следующий пример.
Пример 5. Имеются два проекта с оценками:
,
,
,
,
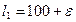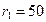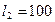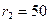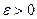-малое число.
Величина централизованного фонда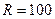 
. Очевидно, что первое предприятие сообщает оценку 
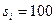(то есть завысит затраты в два раза) и получит финансирование на свой проект. Величина 
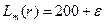, так как при объективных оценках затрат могут финансироваться оба проекта. Имеем
,
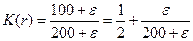то есть эффективность конкурса может быть сколь угодно близка к 0,5.
