Пример 6. а) Отношения «» и «» являются отношениями нестрогого порядка, отношения «<» и «>» – отношениями строгого порядка

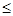а) Отношения «» и «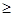» являются отношениями нестрогого порядка, отношения «<» и «>» – отношениями строгого порядка. Оба отношения полностью упорядочивают множества 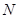и .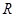

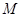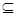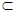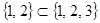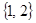б) На системе подмножеств множества отношение включения «» задаёт нестрогий частичный порядок, а отношение строгого включения «» задаёт строгий частичный порядок. Например, , а и 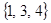не сравнимы.

в) Отношение подчинённости в трудовом коллективе создаёт строгий частичный порядок. В нём, например, несравнимыми являются сотрудники различных структурных подразделений.

Элементы а,b Î М сравнимы по отношению порядка R на М, если выполняется aRb или b Rа.

Множество М, на котором задано отношение порядка, может быть:

а) полностью упорядоченным множеством, если любые два элемента из М сравнимы по отношению порядка. В таком случае говорят, что отношение R задает полный порядок на множестве М. Например, отношение «быть не старше» задает полный порядок на множестве людей;

б) частично упорядоченным множеством - в противном случае. При этом говорят, что отношение R задает на множестве М частичный порядок. Например, отношение «быть начальником» задает на множестве сотрудников организации частичный порядок, так как, например, для пары сотрудников одного отдела данное отношение не выполняется: они несравнимы по данному отношению.