Пример 2. а) Функция является отображением множества натуральных чисел в себя

а) Функция 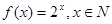является отображением множества натуральных чисел в себя. Эта же функция при всех 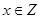является отображением множества целых чисел в множество рациональных чисел.

б) Функция 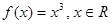является взаимнооднозначным отображением множества действительных чисел на себя.

в) Функция 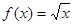не полностью определена, если её тип 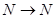, но полностью определена, если её тип 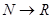или .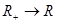

Функции f u g равны,если:

• их области определения - одно и то же множество A,

• для любого а Î A f(a)=g(а).

Функция типа 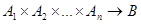называется n-местной функцией. В этом случае принято считать, что функция имеет n аргументов: 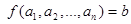, где 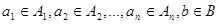. Например, сложение, умножение, вычитание и деление являются двухместными функциями на 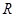, то есть функциями типа .

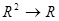Пусть дано соответствие 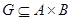. Если соответствие 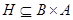таково, что 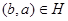тогда и только тогда, когда 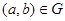, то соответствие 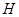называют обратным соответствием к 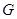и обозначают .

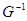Если соответствие, обратное к функции 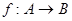является функциональным, то оно называется обратной функцией, обратной к .

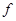В обратном соответствии образы и прообразы меняются местами, поэтому для существования обратной функции 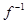требуется, чтобы каждый элемент из области значения 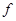имел бы единственный прообраз. Это означает, что для функции 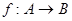обратная функция 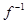существует тогда и только тогда, когда 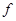является биективным соответствием между своей областью определения и областью значений.

Пусть даны функци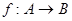и и 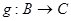. Функция 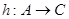называется композицией функци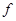й и 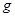(обозначается 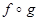), если имеет место равенство: 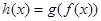, где .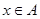

Композиция функци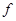й и 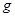представляет собой последовательное применение этих функций; g применяется к результату 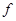.Часто говорят, что функция h получена подстановкой 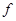в g.

Для многоместных функций 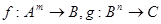возможны различные варианты подстановок 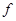в 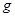, дающие функции различных типов. Особый интерес представляет случай, когда задано множество функций типа: 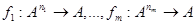. В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых, любые переименования аргументов. Функция, полученная из данных функций 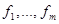некоторой подстановкой их друг в друга и переименованием аргументов, называется их суперпозицией.