Тема 2.1. Логика высказываний

Глава 2. Математическая логика

Резюме по теме

Вопросы для повторения

Пример 7.

Пусть М ₁, - множество сотрудников организации и R₁ - заданное на нем отношение «быть старше»; М ₂ - конечное множество натуральных чисел (ограниченное числом 75) и R ₂ - заданное на нем отношение «быть больше». Гомоморфны или изоморфны модели AЛ1 =(М₁; >) и АЛ2 =(М₂;>)?

Во первых посмотрим гомоморфны ли модели. Определим отображение Г:М₁→ М₂: каждому сотруднику организации из М ₁, поставим в соответствие Г число из М₂, соответствующее его возрасту (в годах). Установленное таким образом отображение Г:М₁→М₂, является гомоморфизмом моделей AЛ1 =(М₁;>) и АЛ2 =(М₂;>), так как выполняется условие (3.2): «если Иванову 37 лет то он старше Петрова 26 лет», т.е. «Иванов > Петро».

Так как Г(«Иванов») = 37 и Г («Петров»)= 26, то и 37 > 26.

Установленное отображение Г:М₁ → М ₂, не является изоморфизмом моделей AЛ1 =(М₁;>) и АЛ2 =(М₂;>), так как не является в общем случае взаимно однозначным (если в организации имеются сотрудники одною возраста, например «Петров» 26 лет и «Сидоров» 26 лет. В этом случае обратное соответствие Г^-1 не является отображением, поскольку не функционально (отсутствует единственность образа 26 на множество сотрудников организации).

Таким образом, заданные модели AЛ1 =(М₁;>) и АЛ2 =(М₂;>) гомоморфны, но не изоморфны.

1.Что называется соответствием?

2.В каком случае соответствие является взаимноодназначным?

3.Что представляет собой гомоморфизм?

4.В чем заключается отличие гомоморфизма и изоморфизма?

5.Дайте определение операции?

6.Каким образом связаны между собой функция и отображение?

7.Перечислите способы задания функции?

8.О чем говорится в теореме Кантора?

9.В каком случае множество называется счетным?

10.Что называется образом и прообразом?

11.Дайте определение мощности множества?

12.Каким образом с помощью взаимнооднозначхых соответствий можно определить мощность множества?

В данной теме рассмотрены понятия соответствие, функция, операция, алгебра, гомоморфизм и так далее. Рассмотрены взаимнооднозначные и не взаимнооднозначные соответствия, а так же понятия алгебры, модели и алгебраической структуры. Дано определение гомоморфизма алгебры и показано в каком случае алгебра может стать изоморфной, то есть обладать свойством изоморфизма.

Математическая логика (теоретическая логика, символическая логика) — раздел математики, изучающий доказательства и вопросы оснований математики. Согласно определению П. С. Порецкого, математическая логика есть логика по предмету, математика по методу. Согласно определению Н.И. Кондакова, математическая логика – вторая, после традиционной логики, ступень в развитии формальной логики, применяющая математические методы и специальный аппарат символов и исследующая мышление с помощью исчислений (формализованных языков). Это определение соответствует определению С.К.Клини: математическая логика – это логика, развиваемая с помощью математических методов. Так же А.А.Марков определяет современную логику «точной наукой, применяющей математические методы». Все эти определения не противоречат, но дополняют друг друга.

Применение в логике математических методов становится возможным тогда, когда суждения формулируются на некотором точном языке. Такие точные языки имеют две стороны: синтаксис и семантику. Синтаксисом называется совокупность правил построения объектов языка (обычно называемых формулами). Семантикой называется совокупность соглашений, описывающих наше понимание формул (или некоторых из них) и позволяющих считать одни формулы верными, а другие — нет.

Важную роль в математической логике играют понятия дедуктивной теории и исчисления. Исчислением называется совокупность правил вывода, позволяющих считать некоторые формулы выводимыми.

Отношение исчислений к семантике выражается понятиями семантической пригодности и семантической полноты исчисления. Исчисление «А» называется семантически пригодным для языка «В», если любая выводимая в «А» формула языка «В» является верной. Аналогично, исчисление «А» называется семантически полным в языке «В», если любая верная формула языка «В» выводима в «А».

Стоит отметить, что на практике множество элементарных логических операций является обязательной частью набора инструкций всех современных микропроцессоров и соответственно входит в языки программирования. Это является одним из важнейших практических приложений методов математической логики.

Логические представления - описание исследуемой системы, процесса, явления в виде совокупности сложных высказываний, составленных из простых (элементарных) высказываний и логических связок между ними.

Цель: ввести логическую терминологию.

Задачи:

1. Рассмотреть понятие логические связки.

2. Рассмотреть основные схемы логически правильных рассуждений.

В математической логике изучаются способы (правила) формального представления высказываний, построения новых высказываний из имеющихся с помощью логически выдержанных преобразований, а также способы (методы) установления истинности или ложности высказываний. Два основных раздела математической логики: логика высказываний и логика предикатов (рис. 2.1), для построения которых существуют два подхода (языка), образующих два варианта формальной логики: алгебру логики и логические исчисления. Между данными подходами имеет место изоморфизм, который характеризуется единством законов логики.

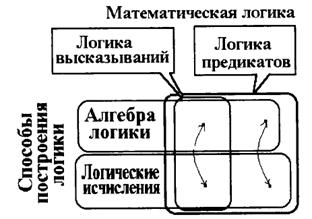
Рис. 2.1. Разделы математической логики и способы их построения

Высказывание - повествовательное предложение (утверждение, суждение), о котором имеет смысл говорить, что оно истинно или ложно.

Пример 1.

Высказываний: «Информационный менеджмент специальность факультета управления и предпринимательства», «Регистрация фирмы требует наличия ее устава», «Рубль - российская валюта», «Все люди смертны».

Истинность или ложность суждения зависит от того, к какой предметной области мы его относим, иными словами в каком контексте употребляем.