Пример 6. Гомоморфизмы и изоморфизмы

Пример 5.

Гомоморфизмы и изоморфизмы

Алгебра – это множество М вместе с заданными на нем операциями { φ₁, φ₂, …, φ_m }. Обозначение алгебры:

AЛ =(M; φ₁, φ₂, …, φ_m),

где М называется основным множествам, а ∑={φ₁, φ₂, …, φ_m} - сигнатурой алгебры AЛ.

Множество натуральных чисел N с операцией умножения * на нем, т.е. AЛ= { N;*).

Типом алгебры AЛ называется вектор арностей операций сигнатуры.

Множество М вместе с заданными на нем отношениями { R ₁, R ₂, …, R _n}называется моделью. Обозначение модели:

MО =(M; R ₁, R ₂, …, R _n),

где М - несущее множество, ∑={R₁, R₂, …, R_n} - сигнатура модели MО.

а) Моделью MО является множество А, чисел с отношениями: «быть больше» и «меньше» MО = (А; >,<);

б) Множество людей В с отношением R - "быть менеджером" задает модель MО = (В; R).

Множество М вместе с заданными на нем операциями {φ₁, φ₂, …,φ_m} и отношениями { R ₁, R ₂, …, R _n}называется алгебраической системой, или алгебраической структурой. Обозначение алгебраической структуры:

АС =(M; φ₁, φ₂, …,φ_m; R ₁, R ₂, …, R _n).

Таким образом, алгебры - это алгебраические структуры с пустым множеством отношений. Другим частным случаем алгебраических структур являются модели, т.е. множества, на которых заданы только отношения.

Пусть между множествами А и В установлено соответствие Г – отображение А в B,т.е. Г: А → В. Это означает, что каждому элементу а из А поставлен в соответствие Г единственный элемент α из В, т.е. Г(а) = α. Пусть также на множестве А задана операция φ, на множестве В - операция ψ, обе одинаковой арности, например обе бинарные, так что a φ b = c, 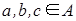, и α ψ β = γ, α,β,γ 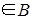. В результате получается две алгебры (А; φ) и (В; ψ).

Тогда отображение Г:А→В называется гомоморфизмом алгебры (А; φ) в алгебру (В; ψ), если выполняется условие:

Г(а φ b) = Г(a) ψ Г(b) (3.1)

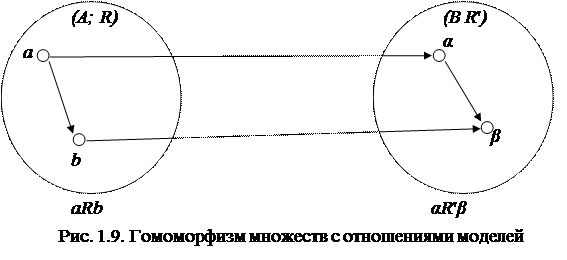
Условие гомоморфизма (3.1) требует (рис. 1.9), чтобы отображение Г результата с = аφb выполнения на множестве А операции φ над элементами а и b, т.е. Г (с) = Г(а φ b), совпадало с результатом γ выполнения на множестве В операции ψ над отображениями этих элементов, т.е. над Г(а) = α и Г(b) =β.

Проверка условия гомоморфизма заключается в следующем. В соответствии с левой частью условия (3.1) сначала над элементами а и b из A должна быть выполнена операция φ, а затем результат с = а φ b выполнения операции φ отображается из А в множество В. В соответствии с правой частью условия (3.1) требуется сначала выполнить отображения элементов a и b из множества A в B, т.е. найти Г (a) =α и Г (b) = β, a затем над α и β выполнить операцию ψ (заданную на множестве В), т.е. Г(а) ψ Г(b), или α ψ β = γ. Условие (3.1) будет выполнено, если результат отображения элемента с = а φ b из А в В совпадает с элементом γ из В, т.е. если Г(с) = γ.

Если при этом отображение Г: А → В является взаимно однозначным соответствием, оно называется изоморфизмом алгебры (А; φ) на алгебру (В; ψ). В этом случае существует и обратное отображение Г^-1: В → А, также взаимно однозначное:

Г^-1(α ψ β) = Г^-1(α) φ Г^-1(β).

Отображение Г^-1 - это изоморфизм В на А. Если существует изоморфизм А на В, то существует изоморфизм В на А. При этом алгебры (А; φ) и (В; ψ) называются изоморфными.

Другими словами, если на множествах А и В заданы несколько операций соответственно (А; φ₁, φ₂, …,φ_m) и (В; ψ₁, ψ₂, …,ψ_m), отображение Г: А→ В является гомоморфизмом алгебры (А; φ₁, φ₂, …,φ_m) в алгебру (В; ψ₁, ψ₂, …,ψ_m), если условия, аналогичные (3.1), выполняются для каждой пары операций φ₁ и ψ₁, …, φ_m и ψ_m.

В силу взаимной однозначности соответствия Г: А → В при изоморфизме мощности основных множеств изоморфных алгебр равны. Поэтому проверка алгебр на изоморфизм сводится к проверке условия гомоморфизма для каждой пары операций и установления взаимной однозначности соответствия Г (равной мощности множеств А и В).

Аналогично определяется гомоморфизм (изоморфизм) множеств с отношениями - моделей (A; R ₁, R ₂, …, R _n) (B; R ₁', R ₂', …, R _n').

Пусть на множестве А задано бинарное отношение R(a,b), где a,b 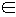А, и на множестве В - бинарное отношение R '(α, β), где α,β 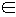В. Тогда отображение Г: А → В является гомоморфизмом модели (А; R) в модель (В; R '), если для любой пары элементов a, b из А такой, что а и b находятся в отношении R следует, что их отображения Г(а) = α и Г(b)= β находятся в отношении R' (рис. 1.10).

a R b влечет Г(а) R' Г(b) для любых а, b 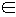А. (3.2)

Если при этом отображение Г: А → В является взаимно однозначным соответствием, оно называется изоморфизмом модели (А; R) на модель (В; R'). В этом случае существует и обратное отображение Г^-1: В → А, также являющееся изоморфизмом: α R' β влечет Г^-1(α) R Г^-1(β) для любых α, β 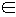В. При этом модели (A: R) и (В: R’) называются изоморфными.

Понятие гомоморфизма (изоморфизма) для алгебраических структур вводится аналогично тому, как это сделано для алгебр и моделей, при этом должны выполняться условия сохранения и операций, и отношений.

Понятие изоморфизма - одно из важнейших понятий в современной математике. Так, из условия изоморфизма следует, например, что любое эквивалентное соотношение в алгебре AЛ сохраняется в любой изоморфной ей алгебре AЛ. Это позволяет, получив такие соотношения в алгебре AЛ, автоматически распространить их на все алгебры, изоморфные AЛ. В частности, изоморфизм сохраняет свойства ассоциативности, коммутативности и дистрибутивности операций, а также рассматриваемые выше свойства отношений.