2014-02-09
887
а) Система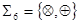 
функционально полна в слабом смысле, так как операция 
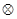нелинейна (как и конъюнкция), а операция 
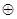(сложение по 
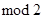) немонотонна.
б) В функционально полной системе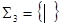 
единственная функция – штрих Шеффера – нелинейна и немонотонна.
Для формулировки необходимых и достаточных условий “cильной” полноты (в отличие от слабой) нужно ввести ряд определений, описывающих ещё три замкнутых класса функций.
Функция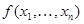 
называется сохраняющей ноль, если выполняется 
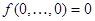и сохраняющей единицу, если выполняется 
.
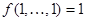Оба данных класса функций являются замкнутыми, что проверяется подстановкой констант в суперпозиции. Равным образом замкнутый класс образуют самодвойственные функции (такие, что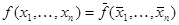 
).
Теорема 6 (вторая – основная – теорема о функциональной полноте). Для того чтобы система функций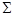 
была функционально полной (в сильном смысле), необходимо и достаточно, чтобы она содержала: 1) нелинейную функцию, 2) немонотонную функцию, 3) функцию, не являющуюся самодвойственной, 4) функцию, не сохраняющую ноль, 5) функцию, не сохраняющую единицу.
