Сколькими способами можно разбить конечное множество Х, где 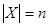 , на подмножества, среди которых для каждого i =1, 2,…, n имеется
, на подмножества, среди которых для каждого i =1, 2,…, n имеется 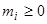 подмножеств с i элементами, где
подмножеств с i элементами, где 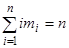 ? Заметим, что в отличие от задачи 1 набор подмножеств в разбиении не является упорядоченным (т.е. порядок подмножеств в разбиении не является существенным). Обозначим число указанных неупорядоченных разбиений множества Х через
? Заметим, что в отличие от задачи 1 набор подмножеств в разбиении не является упорядоченным (т.е. порядок подмножеств в разбиении не является существенным). Обозначим число указанных неупорядоченных разбиений множества Х через 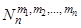 .
.
Теорема 3. 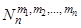
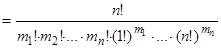 .
.
Доказательство. Каждое из неупорядоченных разбиений, рассмотренных при определении величины 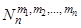 , можно, нумеруя блоки этого разбиения, привести
, можно, нумеруя блоки этого разбиения, привести 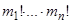 способами к упорядоченным разбиениям вида
способами к упорядоченным разбиениям вида
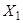 , …,
, …, 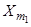 ,
, 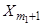 , …,
, …, 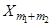 , …,
, …, 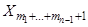 , …,
, …, 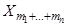 ,
,
где 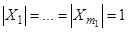 ,
, 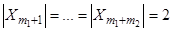 ,…,
,…,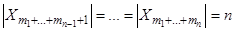 .
.
При этом объединение получаемых таким образом попарно непересекающихся множеств является совокупностью всех возможных разбиений множества Х. Следовательно, по правилу суммы, используя теорему 1, получим:
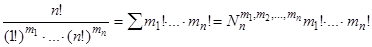
(где суммирование производится по всем рассматриваемым неупорядоченным разбиениям), откуда и следует справедливость доказываемого утверждения.
Пример 4.
Сколькими способами из группы в 25 человек можно сформировать 5 коалиций по 5 человек?
Пусть Х – множество людей в группе, 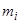 – число коалиций по i человек, где i =1, 2, …, 25. Тогда из условия задачи следует, что
– число коалиций по i человек, где i =1, 2, …, 25. Тогда из условия задачи следует, что 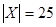 ,
, 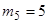 , а для других i
, а для других i 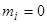 , и, таким образом, искомое число равно
, и, таким образом, искомое число равно 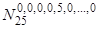
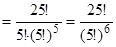 .
.
 2014-02-09
2014-02-09 1937
1937








