Неупорядоченные выборки объемом m из n элементов (m < n) называются сочетаниями. Их число обозначается 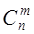 .
.
Теорема 5. 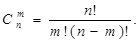
Доказательство. Очевидно, 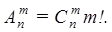 Действительно, объект A – неупорядоченная выборка из n элементов по m, их число
Действительно, объект A – неупорядоченная выборка из n элементов по m, их число 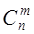 . После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “ A и B “ – упорядоченная выборка.
. После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “ A и B “ – упорядоченная выборка.
Пример 5.
Группа из 15 человек выиграла 3 одинаковых книги. Сколькими способами можно распределить эти книги?
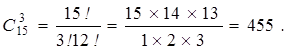
Рассмотрим сочетания, которые не являются подмножествами.
Пусть имеется n типов элементов, каждый тип содержит не менее m одинаковых элементов. Неупорядоченная выборка объемом m из имеющихся элементов (их число ³ m ´ n) называется сочетанием с повторением. Число сочетаний с повторениями обозначается 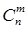 (n).
(n).
Теорема 6. 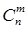 (n) =
(n) = 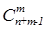 .
.
Доказательство. Пусть в выборку вошло m 1 элементов первого типа, m 2 элементов второго типа,... m n – n -го типа. Причем каждое 0 £ m i £ m и m 1+ m 2+...+ mn = = m. Сопоставим этой выборке вектор следующего вида: 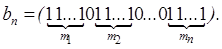 Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов { bn } существует биекция (докажите это!). Следовательно,
Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов { bn } существует биекция (докажите это!). Следовательно, 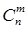 (n) равно числу векторов bn. “ Длина вектора” bn равна числу 0 и 1, или m + + n– 1. Число векторов равно числу способов, которыми m единиц можно поставить на m + n - 1 мест, а это будет
(n) равно числу векторов bn. “ Длина вектора” bn равна числу 0 и 1, или m + + n– 1. Число векторов равно числу способов, которыми m единиц можно поставить на m + n - 1 мест, а это будет 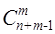 .
.
 2014-02-09
2014-02-09 2147
2147
