Граф H называется частью графа G, H 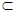 G если V(Н)
G если V(Н) 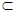 V(G) и E(H)
V(G) и E(H) 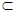 Е(G).
Е(G).
Если V(Н) = V(G), часть H графа G называется суграфом. Суграф является покрывающим для н-графа G если любая вершина графа G инцидентна хотя бы одному ребру из H.
Подграфом G(V’) графа G(V) с множеством вершин V 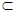 V’ называется часть, которой принадлежат все ребра с обоими концами из V’.
V’ называется часть, которой принадлежат все ребра с обоими концами из V’.
Над частями графа G могут производиться следующие операции:
· дополнение 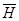 к части H - определяется множеством всех ребер графа G не принадлежащих H: E(H)
к части H - определяется множеством всех ребер графа G не принадлежащих H: E(H) 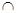 Е(
Е( 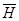 ) =
) = 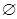 , Е(H)
, Е(H) 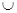 Е(
Е( 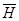 ) = Е(G):
) = Е(G):
· сумма H1 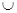 H2 частей H1, и H2 графа G:
H2 частей H1, и H2 графа G:
V (H1 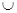 H2)= V(Н1)
H2)= V(Н1) 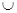 V(H2) и Е(H1
V(H2) и Е(H1 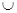 H2)= E(Н1)
H2)= E(Н1) 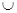 E(H2);
E(H2);
· произведение H1 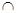 H2:
H2:
V (H1 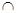 H2)= V(Н1)
H2)= V(Н1) 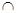 V(H2) и Е(H1
V(H2) и Е(H1 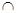 H2)= E(Н1)
H2)= E(Н1) 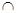 E(H2).
E(H2).
Две части H1 и H2 не пересекаются по вершинам, если они не имеют общих вершин V(Н1) 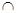 V(H2) =
V(H2) = 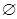 , а значит, и общих ребер E(Н1)
, а значит, и общих ребер E(Н1) 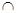 E(H2)=
E(H2)= 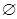 . Части H1 и H2 не пересекаются по ребрам, если E(Н1)
. Части H1 и H2 не пересекаются по ребрам, если E(Н1) 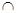 E(H2)=
E(H2)= 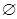 . Если V(Н1)
. Если V(Н1) 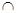 V(H2) =
V(H2) = 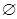 , то сумма H1
, то сумма H1 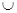 Н2 называется прямой.
Н2 называется прямой.
Графы и бинарные отношения: отношению R, заданному на множестве V, взаимно однозначно соответствует ориентированный граф G(R) без кратных ребер с множеством вершин V, в котором ребро (v', v") существует, только если выполнено v'Rv".
 2014-02-09
2014-02-09 1127
1127








