2014-02-09
1356
Найдем скорость и ускорение, с которым совершается данный колебательный процесс:
 .
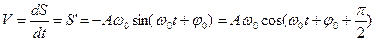| (2.1) | |
 ,
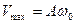| (2.2) |
амплитуда скорости, т.е. скорость изменяется от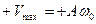 
до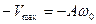 
.
 .
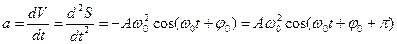| (2.3) | |
 ,
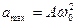| (2.4) |
амплитуда ускорения, т.е. ускорение изменяется от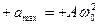 
до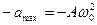 
Сравнивая (2.1) и (1.1) и (2.3) и (1.1) видим, что фаза скоростb отличается от фазы величины S на p/2, а фаза ускорения от фазы величины S на p, т.е. когда S = 0, скорость Vmax, когда S минимально, то аmax.
Построим графики зависимости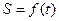 
, 
, 
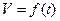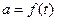(см. рисунки 2.1а, 2.1б, 2.1в).
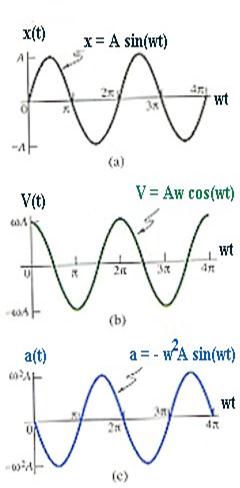
Рис. 2.1.
Перепишем (2.3) так:
 ,
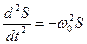| (2.5) |
следовательно
 .
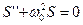| (2.6) |
Уравнение (2.6) называют дифференциальным уравнением гармонических колебаний. Его решением является уравнение (1.1) или (1.1¢).
Графически гармоническое колебание можно изобразить методом вращающегося вектора амплитуды или методом векторных диаграмм.
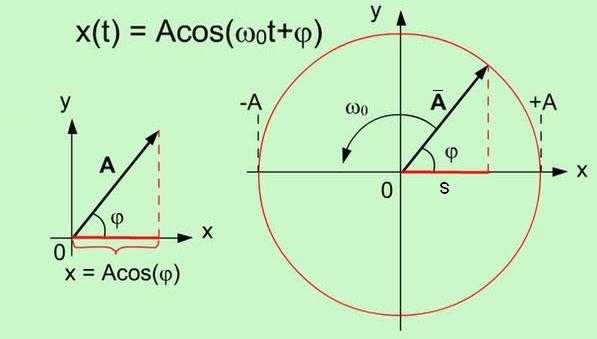
Рис. 2.2. Графическое изображение гармонического колебания методом вращающегося вектора амплитуды
Из произвольной точки О, выбранной на оси х, под углом jо, равным начальной фазе колебания, откладывается вектор `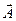
, модуль которого равен амплитуде рассматриваемого колебания. Этот вектор вращают относительно оси, проходящей через точку О с угловой скоростью wо, равной циклической частоте колебаний.
|
|
|
 .
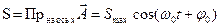| (2.7) |
Проекция конца вектора `А будет перемещаться по оси х и принимать значения от + А до
–А, а колеблющаяся величина S будет изменяться с течением времени по закону: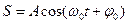 
.
Т.е. гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды `А, отложенного из некоторой произвольной точки О под углом jо, и вращающегося со скоростью wо вокруг этой оси.
Другой способ – представим колеблющуюся величину комплексным числом, по формуле Эйлера:
 ,
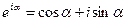| (2.8) |
где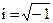 
– мнимая единица/
Любое комплексное число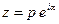 
; 
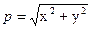; tg a = y / x, где r – модуль комплексного числа.
Тогда уравнение (1.1) запишем в комплексном виде:
 .
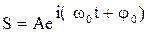| (2.9) |
В декартовой системе координат действительная часть комплексного числа откладывается по оси абсцисс, а мнимая по оси ординат.
Вещественная часть выражения (2.7)
 .
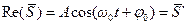| (2.10) |
или
 .
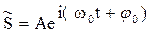| (2.9) |
В теории колебаний принимается, что колеблющаяся величина S равна вещественной части комплексного выражения, стоящего в этом равенстве (2.8) справа.
