Пружинный маятник – груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы: F = – kx, где k – жесткость пружины, х – смещение груза от положения равновесия.
Получим дифференциальное уравнение гармонического колебания пружинного маятника:
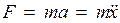
и
F = – kx,
тогда

| (4.2) | |
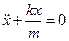
| (4.2¢) |
Сравнив (4.2’) и (4.1)
 , ,
| (4.3) |
тогда
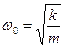 , ,
| (4.4) |
отсюда, учитывая, что wо=2p/Т, получим:
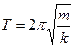
| (4.5) |
период колебаний пружинного маятника.
Формула (4.5) выполняется для упругих колебаний, когда справедлив закон Гука, т.е. когда mпр << mтела.
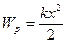
| (4.6) |
потенциальная энергия пружинного маятника.
F упр =-dWp/dx;
-Wp= -kxdx => Wp=kx2/2
F т.упр консервативная сила, тогда
dA = - dWp;
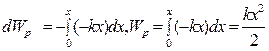 .
.
 2014-02-09
2014-02-09 895
895








