Сложение взаимно перпендикулярных колебаний. Если два складываемых гармонических колебаний одинакового направления мало отличаются по частоте, то возникают биения

Биения

Если два складываемых гармонических колебаний одинакового направления мало отличаются по частоте, то возникают биения.

Биениями называют периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.

Пусть

х₁ = A₁ cos wt

х₂ = A₂ cos (w + Dw) t, тогда х = А¢ cos wt

Амплитуду А¢ найдем по теореме косинусов:

если А₁=А₂ j₀₁= j₀₂= 0 тогда

cos (x+y) = cos x·cos y – sin x·sin y

1 + cos2x = 2cos²x

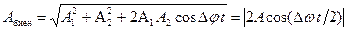	.	(10.4)
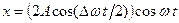		(10.5)

уравнение биений

Т. к. Dw / 2 << w, то (10.5) почти не изменяется за то время, когда cos w t совершит полное колебание частоты изменения амплитуды биения в два раза больше частоты изменения косинуса (т. к. берется по модулю).

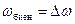(10.6)

тогда частота биений равна разности частот складываемых колебаний.

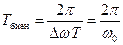(10.7)

График результирующего колебания дают жирные линии, а огибающие их – график изменения с течением времени амплитуды.

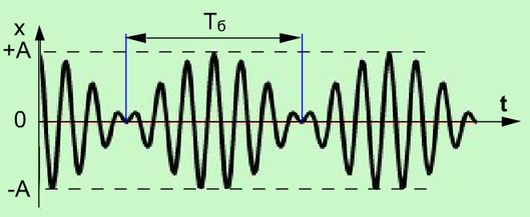
Рис. 10.2. Биения

Метод биений используется для настройки музыкальных инструментов, анализа слуха.

Любые сложные периодические колебания S = f (t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами кратными циклической частоте w_о:

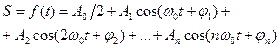(10.8)

Представление периодической функции в виде (10.8) связывают с понятием гармонического анализа сложного периодического колебания или разложения Фурье (Фурье – французский математик).

Слагаемые ряда Фурье, определяющие гармонические колебания с частотами w_о, 2w_о, 3w_о,... называются первой (основной), второй, третьей, и т.д. гармониками сложного периодического колебания.

Пусть имеются два гармонических колебания одинаковой частоты w, происходящие во взаимно перпендикулярных направлениях вдоль осей х и у.

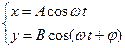(11.1)

j₂– j₁ = j – 0 = j – разность фаз складываемых колебаний.

А и В – амплитуда складываемых колебаний.

Чтобы найти уравнение траектории результирующего колебания у=f (х) необходимо исключить зависимость от t в системе уравнений (11.1).

Пусть из (11.1)

х / А = cos wt;

у /В = cos (wt + j) = cos wt cos j – sin wt sin j,

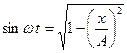
Подставив, получим:

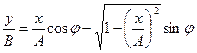Возведем это уравнение в квадрат.

;

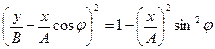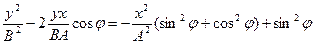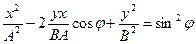(11.2)

Уравнение (11.2) – это уравнение траектории результирующего колебания. Это уравнение эллипса с произвольно ориентированными относительно координатных осей осями.

Если: 1) j = 2mp/2 (m = 0, ±1, ±2,...) то

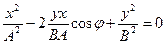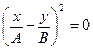	.	(11.3)
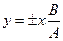	.	(11.4)

Эллипс вырождается в отрезок прямой, где «+» соответствует 0 и четным значениям m (сплошная линия), а «–» нечетным значениям m (пунктирная линия). Результирующее колебание является гармоническими с частотой w и амплитудой:

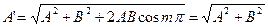(11.5)

Колебание совершается вдоль прямой: у = ± х В / А, которая составляет с осью х угол j

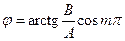(11.6)

Колебания называются линейно поляризованными.

Траектории взаимно перпендикулярных колебаний

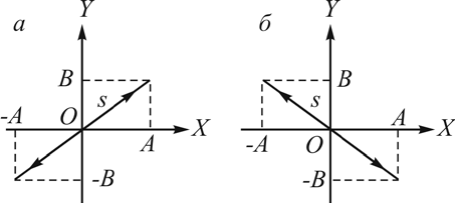
Рис 11.1 – сплошная линия Рис 11.2 – пунктирная линия.

Если: 2) j = (2m + 1) (p / 2) (m = 0, ±1, ±2,...) то уравнение имеет вид:

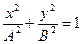(11.6)

это уравнение эллипса, оси которого совпадают с осями координат, а полуоси равны соответствующим амплитудам (рис. 11.3).

Если А = В, то эллипс вырождается в окружность. Такие колебания называются поляризованными по кругу или циркулярно-поляризованными.

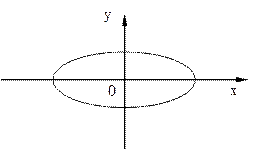
Рис. 11.3

Если частоты складываемых, взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания имеем сложный вид и носит названия фигур Лиссажу. Ж. Лиссаж – (1822-1880) – французский физик (см. рис. 11.4.)

Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельным осям координат. По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Метод фигур Лиссажу используют для анализа соотношений частот и разности фаз складываемых колебаний.