Свободные затухающие колебания в электрическом колебательном контуре

Если в колебательном контуре R ¹ 0, то дифференциальное уравнение свободного затухающего колебания заряда в контуре имеет вид:

,

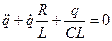(7.21)

сравнивая с уравнением 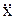+ 2d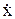+ w²_о = 0 имеем

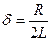	,	(7.22)
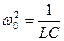	.	(7.23)

Решением (7.21) является функция:

,

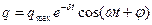(7.24)

a

,

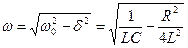(7.25)

w<w_о.

Если R = 0, то w = w_о =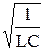

Логарифмический декремент определяется так:

,

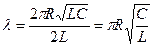(7.26)

а добротность

.

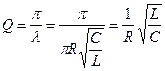(7.27)

C ростом d растет и период затухающих колебаний и при d = w_о Т = =¥, колеблющаяся величина асимптотически приближается к 0, когда t ® ¥. Процесс перестает быть периодическим.

Оказывается возможно поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии в реальной колебательной системе. Особенно широко применяются автоколебания.

Автоколебания - незатухающие колебания, поддерживаемые в колебательной системе за счет постоянного внешнего источника энергии, а свойства этих колебаний определяются самой системой.

Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии нужными порциями в нужный момент. Примером автоколебательной системы могут служить часы. Механизм подталкивает маятник в такт с его колебаниями.

Энергия, передаваемая при этом берется либо за счет раскручивающийся пружины, либо за счет опускающегося груза. Автоколебательными системами являются также ДВС, паровые турбины, ламповый генератор.