Пусть дан вектор 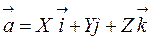 . Единичный вектор того же направления, что и
. Единичный вектор того же направления, что и 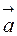 (орт вектора
(орт вектора 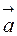 ) находится по формуле:
) находится по формуле:
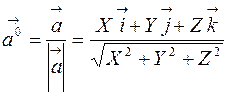 .
.
Пусть ось 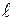 образует с осями координат углы
образует с осями координат углы 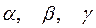 . Направляющими косинусами оси
. Направляющими косинусами оси 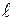 называются косинусы этих углов:
называются косинусы этих углов: 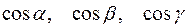 . Если направление
. Если направление 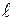 задано единичным вектором
задано единичным вектором 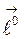 , то направляющие косинусы служат его координатами, т.е.
, то направляющие косинусы служат его координатами, т.е.
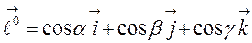 .
.
Направляющие косинусы связаны между собой соотношением
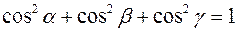 .
.
Если направление 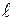 задано произвольным вектором
задано произвольным вектором 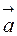 , то находят орт этого вектора и, сравнивая его с выражением для единичного вектора
, то находят орт этого вектора и, сравнивая его с выражением для единичного вектора 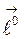 , получают:
, получают:
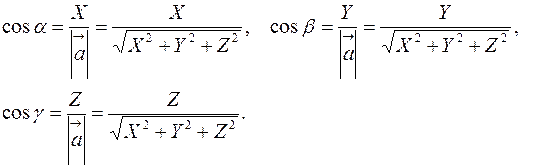
 2014-02-09
2014-02-09 792
792








