2014-02-09
565
Число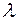 
называется собственным значением (или характеристическим числом) квадратной матрицы 
порядка 
, если можно подобрать такой –мерный ненулевой вектор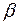 
, что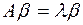 
.
Для того, чтобы найти собственные значения матрицы , рассмотрим матрицу
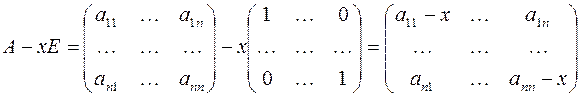
Если раскрыть определитель матрицы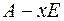 
, то получится многочлен –й степени:
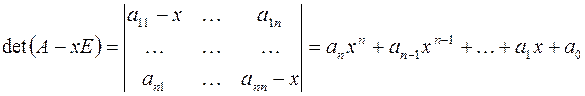
Этот многочлен называется характеристическим многочленом матрицы . Его коэффициенты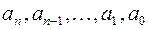 
зависят от элементов матрицы . Понятие многочлена будет подробно разобрано в следующем разделе.
Следует отметить, что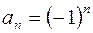 
, 
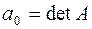. Уравнение 
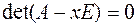называется характеристическим уравнением матрицы .
Теорема. Множество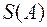 
всех собственных значений матрицы совпадает с множеством всех решений характеристического уравнения 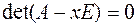матрицы .
Доказательство: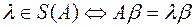 
, 
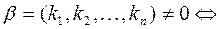
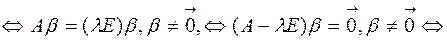
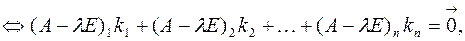
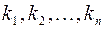– ненулевой набор чисел, 
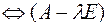– вырожденная матрица 
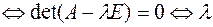– решение уравнения
.
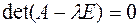Собственным вектором квадратной матрицы порядка , принадлежащим ее собственному значению 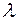называется -мерный вектор 
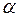, для которого 
.
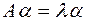Множество всех собственных векторов матрицы , принадлежащих ее собственному значению 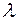, обозначим через 
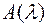. Отыскание собственных векторов сводится к решению однородной системы линейных уравнений.
|
|
|
Теорема. Множество 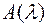всех собственных векторов матрицы порядка , принадлежащих ее собственному значению 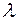, совпадает с множеством всех решений однородной системы линейных уравнений 
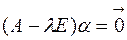, где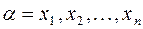 
Доказательство: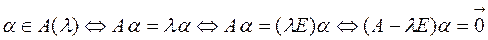 
В развернутом виде равенство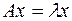 
записывается как система уравнений:
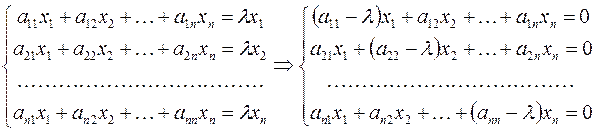
Если зафиксировано число 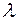, то задача нахождения собственного вектора матрицы сводится к поиску ненулевого решения системы линейных однородных уравнений с неизвестными 
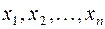, которые являются координатами вектора 
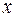. Эта система имеет ненулевое решение только тогда, когда выполняется условие
,
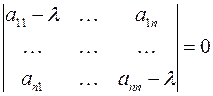т.е. число 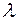является собственным числом матрицы .
Знание всех собственных векторов матрицы позволяет решить задачу диагонализации этой матрицы, то есть нахождения треугольной или диагональной матрицы, имеющий такие же собственные значения.
