Теорема. Если и – два различных собственных значения симметрической матрицы , то соответствующие им собственные векторы и удовлетворяют соотношению , т.е. они ортогональны

Теорема. Предположим, что квадратная матрица -го порядка имеет линейно независимых собственных векторов. Тогда если взять эти векторы в качестве столбцов матрицы, то матрица будет диагональной матрицей, у которой на диагонали стоят собственные значения матрицы, т.е.

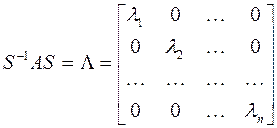
Таким образом собственные значения симметрической матрицы различны, а, значит, если пронормировать соответствующие им собственные векторы, то система собственных векторов матрицы станет ортонормированной, а матрица 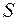, столбцами которой будут эти векторы, станет ортогональной.

Ортогональной называется вещественная квадратная матрица, у которой соответствующая ей система векторов-столбцов является ортонормированной системой евклидова пространства.

Теорема. Матрица является ортогональной тогда и только тогда, когда .

В соответствии с этой теоремой 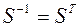, и преобразование 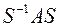эквивалентно преобразованию

При определении характеристических чисел матрицы было введено новое понятие характеристического многочлена. Подробный анализ понятия многочлена приводится в следующем разделе.