Лекция 11. Многочлены
Контрольные вопросы к теме
1. Переход к новому базису и понятие матрицы перехода.
2. Понятие линейного оператора.
3. Собственные значения и собственные вектора матрицы.
4. Операция диагонализации матрицы и понятие ортогональной матрицы.
Основные понятия, включенные в систему тренинг- тестирования:
многочлен; степень многочлена; коэффициенты; старший коэффициент; сложение многочленов; умножение многочленов; делитель; частное; остаток; корень многочлена; кратность корня многочлена; линейные многочлены; схема Горнера; рациональная дробь; правильная рациональная дробь; простейшие (или элементарные) дроби; метод неопределенных коэффициентов.
Многочленом от переменной 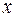 степени
степени  называется выражение вида
называется выражение вида

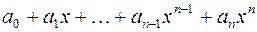 ,
,
где 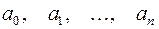 ‑ действительные или комплексные числа, называемые коэффициентами,
‑ действительные или комплексные числа, называемые коэффициентами,  ‑ натуральное число,
‑ натуральное число, 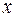 ‑ переменная величина, принимающая произвольные числовые значения.
‑ переменная величина, принимающая произвольные числовые значения.
Если коэффициент 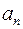 при
при 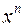 многочлена
многочлена 
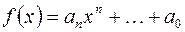 отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число
отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число  называется степенью многочлена,
называется степенью многочлена, 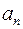 – старшим коэффициентом, а
– старшим коэффициентом, а 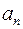
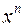 – старшим членом многочлена. Коэффициент
– старшим членом многочлена. Коэффициент 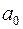 называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.
называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 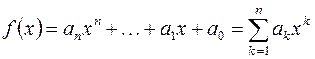 и
и 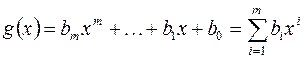 ,
, 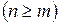 называется многочлен
называется многочлен 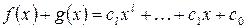 , где
, где 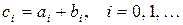
Произведением многочленов 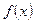 и
и 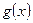 называется многочлен
называется многочлен
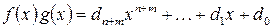
где 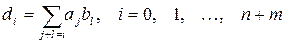 .
.
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 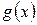 называется делителем многочлена
называется делителем многочлена 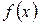 , если существует многочлен
, если существует многочлен 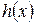 такой, что
такой, что 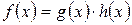 .
.
 2014-02-09
2014-02-09 475
475








