Функциональная полнота

Система функций, суперпози­цией которых может быть представлена любая функция из неко­торого множества булевых функций, называется функционально пол­ной. Если в такой системе допускаются константы 0 и 1, то ее назы­вают ослабленно функционально полной. Говорят, что функционально полная система функций образует базис в логическом пространстве. Система функций называется минимально полным базисом, если удаление из нее любой функции превращает эту систему в не­полную.

Рассмотренные в (9.4) функционально полные системы комплек­товались путем сопоставления различных выражений для булевых функций. Общее решение вопроса основано на теореме о функцио­нальной полноте: для того чтобы система булевых функций была полной, необходимо и достаточно, чтобы она включала хотя бы одну функцию: не сохраняющую константу 0, не сохраняющую констан­ту 1, несамодвойственную, нелинейную и немонотонную. Эту теорему следует понимать так, что одна и та же функция может представлять в функционально полной системе одно илинесколько требуемых свойств, если она обладает этими свойствами.

С помощью табл. 9.1 можно следующим образом охарактеризовать свойства булевых функций с позиций функциональной полноты (звездочкой отмечены свойства, которыми обладает данная функ­ция:

Таблица 10.1 - Свойства булевых функций

Булевы функции	Формулы	Свойства
Несохранение 0	Несохранение 0	Несамодвойст-венность	Нелинейность	Немонотонность
Константа 0			*	*
Константа 1		*		*
Отрицание		*	*			*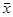
Конъюнкция				*	*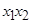
Дизъюнкция				*	*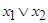
Импликация		*		*	*	*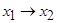
Эквиваленция		*		*		*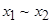
Отрицание импликации			*	*	*	*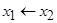
Сумма по модулю 2			*	*		*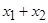
Штрих Шеффера		*	*	*	*	*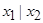
Стрелка Пирса		*	*	*	*	*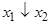

Отсюда видно, что рассмотренные в (9.4) системы операций (дизъюнкция и отрицание, конъюнкция и отрицание, штрих Шеффера, стрелка Пирса) удовлетворяют теореме о функциональной полноте. Система операций алгебры Жегалкина (сумма по модулю 2 и конъюнкция) вместе с константой 1 образует ослабленно функ­ционально полную систему.

Выбрав любую элементарную функцию и дополнив ее одной или несколькими другими функциями так, чтобы все они вместе удовлет­воряли теореме о функциональной полноте, можно выразить через них все другие булевы функции. Например, в основу одного из та­ких комплектов можно положить импликацию и константу 0. Тогда 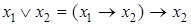и 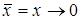, а через дизъюнкцию и отрицание выразятся и все остальные функции. В качестве дру­гого функционально полного комплекта можно взять конъюнкцию, эквиваленцию и константу 0. При этом 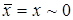и формулы алгебры логики, построенной на этих операциях, будут двой­ственны формулам алгебры Жегалкина, если в качестве двойствен­ных символов принять + и ~, а также 1 и 0.

По-видимому, все лучшее, что можно извлечь из различных ва­риантов функционально полных систем, уже заложено в булевой алгебре и алгебре Жегалкина. Но при решении специальных задач не исключается построение и применение других алгебр логики.